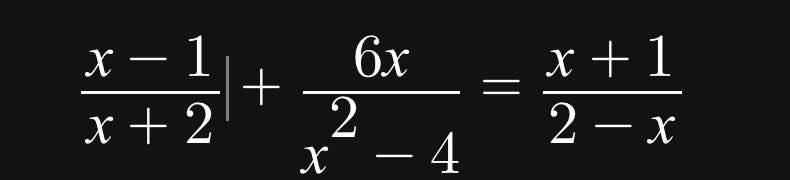\(\dfrac{x-1}{x+2}+\dfrac{6x}{x^2-4}=\dfrac{x+1}{2-x}\left(dkxd:x\ne\pm2\right)\)

\(\Leftrightarrow\dfrac{x-1}{x+2}+\dfrac{6x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{x+1}{x-2}\)

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)+6x+\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)

\(\Leftrightarrow x^2-2x-x+2+6x+x^2+2x+x+2=0\)

\(\Leftrightarrow2x^2+6x+4=0\)

\(\Leftrightarrow2x^2+2x+4x+4=0\)

\(\Leftrightarrow2x\left(x+1\right)+4\left(x+1\right)=0\)

\(\Leftrightarrow\left(2x+4\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)

Vậy \(S=\left\{-1\right\}\)

`@` `\text {Ans}`

`\downarrow`

`a)`

Thu gọn:

`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)

`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`

`= -x^5 + 5x^4 + 2x^2 + 2x - 4`

`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)

`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`

`= x^5 - x^4 - x^3 - x^2 + 7x - 2`

`@` Tổng:

`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)

`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`

`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`

`= 4x^4 - x^3 + x^2 + 9x - 6`

`@` Hiệu:

`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)

`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`

`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`

`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`

`b)`

`@` Thu gọn:

\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)

`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`

`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`

`= x^4 - 2x^3 - x^2 + 15x + 10`

\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)

`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`

`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`

`= x^4 + 3x^3 + 2x - 4`

`@` Tổng:

`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)

`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`

`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`

`= 2x^4 + x^3 - x^2 + 17x + 6`

`@` Hiệu: 

`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)

`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`

`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`

`= -5x^3 - x^2 + 13x + 14`

`@` `\text {# Kaizuu lv u.}`

Gọi số cây trồng đc trong ngày đầu lớp 5A là a ( a ϵ N*, cây )

số cây trồng đc trong ngày đầu lớp 5B là \(\dfrac{3}{2}\)a ( cây )

số cây trồng đc trong ngày 2 lớp 5A là a + 80 ( cây )

số cây trồng đc trong ngày 2 lớp 5B là \(\dfrac{3}{2}\)a + 60 ( cây )

Vì ngày thứ 2 lớp 5A trồng bằng \(\dfrac{3}{4}\) lớp 5B nên ta có :

\(a+80=\dfrac{3}{4}\left(\dfrac{3}{2}a+60\right)\)

\(a+80=\dfrac{9}{8}a+45\)

\(80-45=\dfrac{9}{8}a-a\)

\(35=\dfrac{1}{8}a\)

\(a=280\left(cây\right)\)

→ Số cây lớp 5A trồng ngày đầu là: 280 cây

→ Số cây lớp 5B trồng ngày đầu là : \(\dfrac{3}{2}a=\dfrac{3}{2}280=420\left(cây\right)\)

Đề chưa đúng, em chỉnh lại đề nhé!

a, Tỉ số phần trăm số cây đã trồng cho với dự kiến kế hoạch là:

(2052/1520) x 100% = 135%

b, Xã A vượt mức kế hoạch với tỉ lệ:

135% - 100% = 35%

c, Nếu xã A trồng vượt mực 2,5% so với kế hoạch thì xã A đã trồng vượt mức số lượng cây là:

2,5% x 1520= 38 (cây)

Đáp số: a, 135%

b, 35%

c, 38 cây

2xy-2x3y=-9

(2x+3)y-2x-(-9)=0

(2x+3)y-2x+9=0

2x+3=0

2(y-1)=0

2y=2

y=1

mình cũng không rõ lắm í tại vì hè này mình mới lên lớp 6 mình cũng biết sơ sơ

a) Ta có:

A = (a - 1)x^3 + 4x^2 + 8x + 1

b) Ta có:

B = mx^4 - 3x^4 + 3

B = (m - 3)x^4 + 3

Vậy đáp án là:

a) A = (a - 1)x^3 + 4x^2 + 8x + 1

b) B = (m - 3)x^4 + 3

\(\widehat{A}+\widehat{D}=70^o+110^o=180^o\) 

=> ABCD là tứ giác nội tiếp (tứ giác có tổng 2 góc đối =180 là tứ giác nt)

\(\widehat{ABD}=\widehat{ACD}\) (góc nt cùng chắn cung AD) (1)

\(\widehat{CBD}=\widehat{CAD}\) (góc nt cùng chắn cung CD) (2)

Tg ADC cân tại D \(\Rightarrow\widehat{ACD}=\widehat{CAD}\) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{ABD}=\widehat{CBD}\)

\(a,\left(x-2\right)\left(3x-1\right)=x\left(2-x\right)\)

\(\Leftrightarrow\left(x-2\right)\left(3x-1\right)+x\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(3x-1+x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\4x-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{4}\end{matrix}\right.\)

Vậy \(S=\left\{\dfrac{1}{4};2\right\}\)

\(b,\left|2x+3\right|=4x+1\)

\(TH_1:x\ge-\dfrac{3}{2}\)

\(2x+3=4x+1\\ \Leftrightarrow-2x=-2\\ \Leftrightarrow x=1\left(tm\right)\)

\(TH_2:x< -\dfrac{3}{2}\)

\(-2x-3=4x+1\\ \Leftrightarrow-6x=4\Leftrightarrow x=-\dfrac{2}{3}\left(ktm\right)\)

Vậy \(S=\left\{1\right\}\)

\(c,\dfrac{x+1}{3}+1=3-\dfrac{5x}{10}\\ \Leftrightarrow\dfrac{10\left(x+1\right)+30-90+15x}{30}=0\\ \Leftrightarrow10x+10-60+15x=0\\ \Leftrightarrow25x=50\\ \Leftrightarrow x=2\)

Vậy \(S=\left\{2\right\}\)

\(d,\dfrac{1}{x+2}+\dfrac{3}{2-x}=\dfrac{2x-3}{x^2-4}\left(dk:x\ne\pm2\right)\)

\(\Leftrightarrow\dfrac{x-2-x-2-2x+3}{x^2-4}=0\)

\(\Leftrightarrow-2x=1\)

\(\Leftrightarrow x=-\dfrac{1}{2}\left(tmdk\right)\)

Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)

Câu d, Sửa từ dòng 2 :

\(\Leftrightarrow\dfrac{x-2-3x-6-2x+3}{x^2-4}=0\)

\(\Leftrightarrow-4x=5\)

\(\Leftrightarrow x=-\dfrac{5}{4}\left(tm\right)\)

Vậy ...