Cho đa thức R(x)=x^2 + 3x
a)số nào sau đây là nghiệm của đa thức :-1,-2,-3
b)tìm các nghiệm của R(x)
MIK CẢM ƠN BẠN RẤT NHIỀU !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x+4}{2014}+\dfrac{x+3}{2015}=\dfrac{x+2}{2016}+\dfrac{x+1}{2017}\)
\(\dfrac{x+4}{2014}+1+\dfrac{x+3}{2015}+1=\dfrac{x+2}{2016}+1+\dfrac{x+1}{2017}+1\)
\(\dfrac{x+2018}{2014}+\dfrac{x+2018}{2015}=\dfrac{x+2018}{2016}+\dfrac{x+2018}{2017}\)
\(\left(x+2018\right)\left(\dfrac{1}{2014}+\dfrac{1}{2015}-\dfrac{1}{2016}-\dfrac{1}{2017}\right)=0\\ x+2018=0\\ x=-2018\)


câu a :
xét ΔAMB và ΔDMC, ta có :
MB = MC (vì M là trung điểm của BC)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
MA = MD (giả thiết)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
câu b :
\(vì\) \(\Delta AMB=\Delta DMC\) \(nên\) \(\Rightarrow\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên => AB // DC
câu a :
xét \(\Delta ADM\) và \(\Delta DMC\), ta có :
\(MB=MC\) (vì M là trung điểm của cạnh BC)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(MA=MD\) (giả thiết)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
câu b :
vì \(\Delta AMB=\Delta DMC\) nên \(\Rightarrow\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng). Mà 2 góc này ở vị trí soletrong nên AB // DC

\(a,x^2-2=0\Leftrightarrow x^2-\left(\sqrt{2}\right)^2=0\Leftrightarrow\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy \(S=\left\{-\sqrt{2};\sqrt{2}\right\}\)
\(b,x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{0;2\right\}\)
\(c,x^2-2x=0\Leftrightarrow x\left(x-2\right)\) phương trình như câu b,
\(d,x\left(x^2+1\right)\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=-1\left(voli\right)\end{matrix}\right.\)( voli là vô lí )
Vậy \(S=\left\{0\right\}\)
Tìm 3 số a,b,c biết rằng : a+b+c= 29 , a và b tỉ lệ nghịch với 3 và 2, b và c tỉ lệ thuận với 4 và 3

Lời giải:
Theo bài ra ta có:
$3a=2b; \frac{b}{4}=\frac{c}{3}$
$\Rightarrow \frac{a}{8}=\frac{b}{12}=\frac{c}{9}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{8}=\frac{b}{12}=\frac{c}{9}=\frac{a+b+c}{8+12+9}=\frac{29}{29}=1$
$\Rightarrow a=8.1=8; b=12.1=12; c=9.1=9$

Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\) \(\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{z}{15}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
Lại có:
\(\dfrac{z}{15}=\dfrac{4z}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{4z}{60}=\dfrac{x+4z}{20+60}=\dfrac{240}{80}=3\)
\(\Rightarrow x=3\cdot20=60\)
\(y=3\cdot10=30\)
\(z=3\cdot15=45\)

Ta có: ∠BAC + ∠DAC = 180° ( kề bù )
mà ∠BAC = 90° (gt)
⇒ ∠DAC = 180° - 90° = 90°
⇒ ∠BAC = ∠DAC
Xét ∆ABC và ∆ADC có: AB = AC (gt) ; ∠BAC = ∠DAC (cmt) ; AC chung
⇒ ∆ABC = ∆ADC ( c_g_c)
⇒ BC = DC ( 2 cạnh tương ứng )
⇒ ∆CBD cân tại C ( theo dhnb)
Chú thích:
gt: giả thiết
theo dhnb: dấu hiệu nhận biết
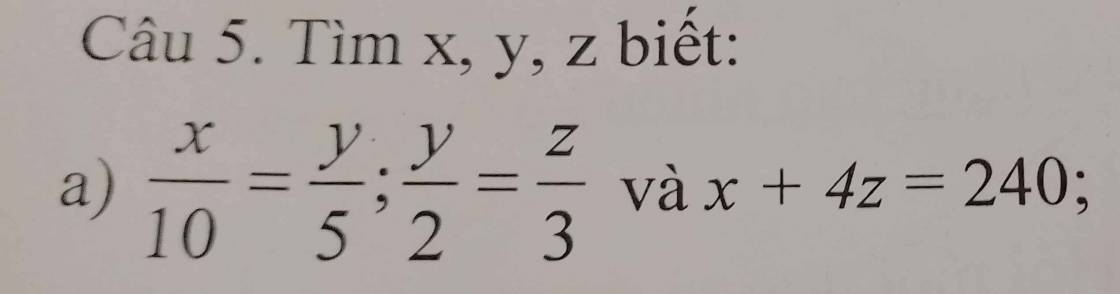
\(R\left(x\right)=x^2+3x\)
a) Ta có:
\(R\left(x\right)=x^2+3x\)
\(R\left(x\right)=x\left(x+3\right)\)
\(R\left(x\right)=x\left(x+3\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x+3=0\Rightarrow x=-3\end{matrix}\right.\)
Vậy: Trong các số -1, -2 và -3 thì nghiệm của đa thức là -3
b) Các nghiệm của R(x) là 0 và -3 (ở phần a)
cảm ơn nha