Bài học cùng chủ đề
- Xét tính đơn điệu khi biết đồ thị hàm số hoặc bảng biến thiên
- Xét tính đơn điệu khi biết công thức hàm số (hoặc đạo hàm)
- Xét tính đơn điệu của hàm số chứa tham số
- Tìm cực trị của hàm số khi biết bảng biến thiên hay đồ thị hàm số
- Tìm cực trị của hàm số khi biết công thức hàm số (hoặc đạo hàm)
- Xét tính đơn điệu của hàm số
- Xét tính đơn điệu của hàm số chứa tham số
- Xác định cực trị của hàm số
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Xác định cực trị của hàm số SVIP
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau:
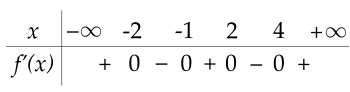
Số điểm cực đại của hàm số đã cho là
Cho hàm số y=f(x) có đạo hàm trên R và có bảng biến thiên như sau:
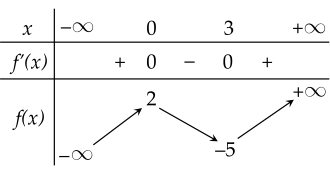
Giá trị cực đại của hàm số đã cho bằng
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau:
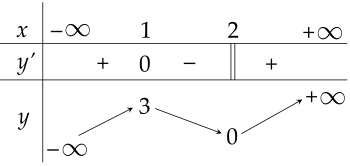
Điểm cực tiểu của đồ thị hàm số là
Cho hàm số y=f(x) xác định trên R\{x2} và có bảng xét dấu của đạo hàm như sau.
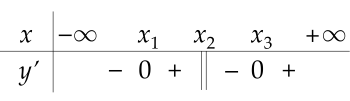
Khi đó số cực trị của hàm số y=f(x) là
Số điểm cực trị của hàm số y=x+12x+3 là
Cho hàm số y=f(x) có đạo hàm f′(x)=(x−1)(2−x), ∀x∈R. Điểm cực đại của hàm số là
Điểm cực tiểu của hàm số y=x3−12x+1 là
Cho hàm số y=f(x) có đồ thị hàm số đạo hàm y=f′(x) như trong hình vẽ.
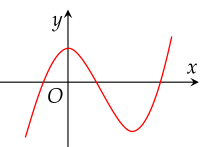
Số điểm cực trị của hàm số y=f(x) là
Số điểm cực trị của hàm số y=34x3−2x2−x−3 là
Trong các hàm số dưới đây, hàm số nào không có cực trị?
Hàm số y=∣x∣+2 có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) có đạo hàm f′(x)=x2(x2−25),x∈R.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số đã cho có 3 điểm cực trị. |
|
| b) Hàm số đã cho đạt cực tiểu tại x=5. |
|
| c) Hàm số đã cho nghịch biến trên khoảng (−∞;−5). |
|
| d) Hàm số đã cho đạt cực đại tại x=−5. |
|
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên
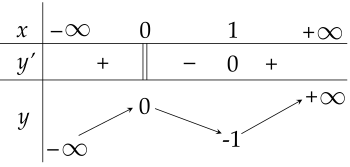
| a) Hàm số y=f(x) có giá trị cực tiểu bằng 1. |
|
| b) Đồ thị hàm số y=f(x) có điểm cực tiểu là (1;−1). |
|
| c) Hàm số y=f(x) đạt cực đại tại x=0. |
|
| d) Hàm số y=f(x) có đúng một cực trị. |
|
Cho hàm số y=f(x) liên tục trên R và đồ thị của hàm số y=f′(x) như hình vẽ dưới đây.
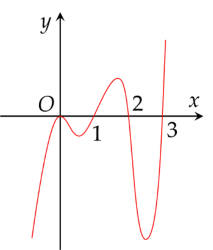
Hàm số đã cho đạt cực đại tại điểm
Hàm số y=f(x) có đạo hàm y=f′(x) liên tục trên R và có đồ thị như hình dưới đây.
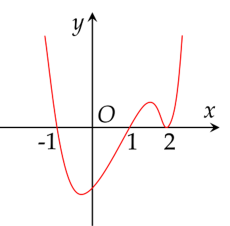
Số điểm cực đại của hàm số y=f(x) là


Bạn có thể đánh giá bài học này ở đây