Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen SVIP

I. Vectơ quay

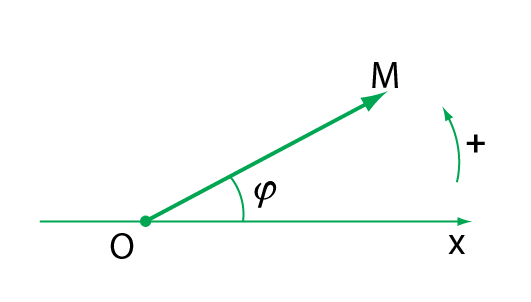
Khi điểm \(M\) chuyển động tròn đều thì vectơ vị trí \(\overrightarrow{OM}\) quay đều với cùng tốc độ góc \(\omega\).

Phương trình của hình chiếu của vectơ quay \(\overrightarrow{OM}\) lên trục \(x\) là

\(x=A\cos\left(\omega t+\varphi\right)\)

Vectơ quay \(\overrightarrow{OM}\) có các đặc điểm sau

• Có gốc tại gốc tọa độ của trục \(Ox\)
• Có độ dài bằng biên độ dao động \(OM=A\)
• Hợp với trục \(Ox\) một góc bằng pha ban đầu

II. Phương pháp giản đồ Fre-nen

Giả sử có hai dao động điều hòa cùng phương, cùng tần số

\(x_1=A_1\cos\left(\omega t+\varphi_1\right)\)

\(x_2=A_2\cos\left(\omega t+\varphi_2\right)\)

Phương pháp giản đồ Fre-nen giúp tìm được phương trình dao động tổng hợp của hai dao động này.

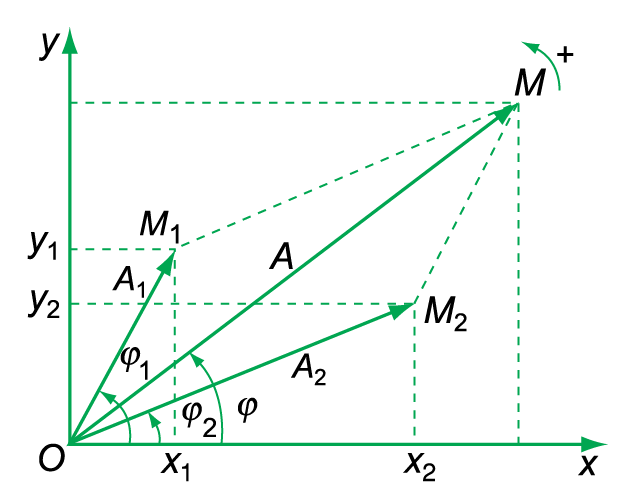
• Vẽ vectơ quay \(\overrightarrow{OM_1}\) và \(\overrightarrow{OM_2}\) biểu diễn hai li độ \(x_1\) và \(x_2\)
• Vẽ vectơ \(\overrightarrow{OM}\) là tổng của hai vectơ trên. Sử dụng quy tắc hình bình hành ta thấy vectơ đường chéo \(\overrightarrow{OM}\) cũng là một vectơ quay với tốc độ góc \(\omega\) quanh gốc tọa độ \(O\). 
• Vectơ quay \(\overrightarrow{OM}\) biểu diễn phương trình dao động điều hòa tổng hợp \(x=A\cos\left(\omega t+\varphi\right)\)

• Biên độ của dao động tổng hợp được tính theo công thức

• Pha ban đầu \(\varphi\) của dao động tổng hợp được tính theo công thức

III. Ảnh hưởng của độ lệch pha

Biên độ dao động tổng hợp phụ thuộc và

• Biên độ dao động \(A_1\) và \(A_2\)
• Độ lệch pha \(\left(\varphi_2-\varphi_1\right)\) của dao động thành phần

Nhận xét:

• Nếu hai dao động thành phần cùng pha \(\left(\Delta\varphi=0\right)\) thì biên độ dao động tổng hợp lớn nhất

\(A=A_1+A_2\)

• Nếu hai dao động thành phần ngược pha \(\left(\Delta\varphi=\pi\right)\) thì biên độ dao động tổng hợp nhỏ nhất

\(A=\left|A_1-A_2\right|\)