Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Tính chất đường phân giác của tam giác SVIP
00:00
1. ĐỊNH LÍ
- Tính chất đường phân giác của tam giác

Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
- Ví dụ: $AD$ là đường phân giác của tam giác $ABC$ nên $\dfrac{BD}{CD} = \dfrac{AB}{AC}$.
2. CHỨNG MINH ĐỊNH LÍ
Vẽ đường thẳng qua $B$, song song với $AD$, cắt đường thẳng $AC$ tại $E$.
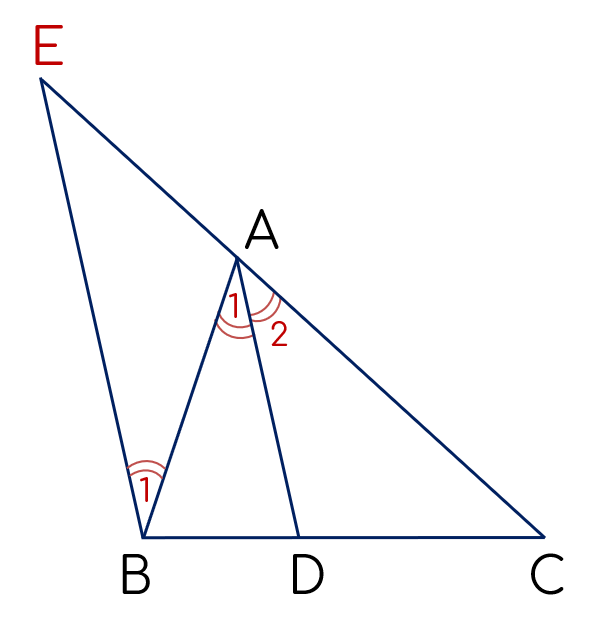
Theo giả thiết, $AD$ là phân giác của góc $A$ nên $\widehat{A_1} = \widehat{A_2}$.
Ta có $EB$ // $AD$ nên $\widehat{A_1} = \widehat{B_1}$ (hai góc so le trong);
$\widehat{A_2} = \widehat{E}$ (hai góc đồng vị).
Do đó, $\widehat{B_1} = \widehat{E} (= \widehat{A_1} = \widehat{A_2})$ nên tam giác $AEB$ cân tại $A$.
Suy ra $AE = AB$ (1)
Mặt khác, áp dụng định lí Thalès vào tam giác $CEB$, ta có:
$\dfrac{DB}{DC} = \dfrac{AE}{AC}$ (2)
Từ (1) và (2) suy ra $\dfrac{DB}{DC} = \dfrac{AB}{AC}$.
3. LUYỆN TẬP – VẬN DỤNG
@201237343432@@201237373580@
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây