Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tìm giao tuyến của hai mặt phẳng SVIP
Cho B là một điểm không thuộc mặt hình thang KHMQ(KH//MQ và KH>MQ). Gọi C là điểm của KQ và HM. Khi đó giao tuyến của (BKQ) và (BHM) là
Cho hình chóp S.ABCD. O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAO) và (SBC) là đường thẳng
Cho tứ diện MNPQ. A,B lần lượt là trung điểm của PQ và MQ, G là trọng tâm tam giác MPQ. NG là giao tuyến của hai mặt phẳng nào dưới đây?
Trong mp(α), cho tứ giác ABCD. AB cắt CD tại I, AC cắt BD tại O. Lấy điểm S là điểm không thuộc (α).
Gọi M, N lần lượt là giao điểm của IO với AD và BC. Giao tuyến của (SIO) với (SAD) là
Cho hình chóp S.ABCD đáy hình vuông tâm O. E là điểm nằm trên cạnh SC (E không trùng với S và C). Gọi I là giao điểm của AE và mặt phẳng (SBD). Khẳng định nào sau đây là đúng?
Cho tứ diện ABCD, M là trung điểm của AB, N là điểm trên AC mà AN=41AC, P là điểm trên đoạn AD mà AP=2PD . Gọi E là giao điểm của MP và BD, F là giao điểm của MN và BC. Khi đó giao tuyến của (BCD) và (FMP) là :
Cho hình lập phương ABCD.A′B′C′D′ (các đỉnh lấy theo thứ tự đó). AC∩BD=O, A′C′∩B′D′=O′. Khi đó giao tuyến của hai mặt phẳng (ACC′A′) và (AB′D′) là đường thẳng nào sau đây?
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AC và CD. Giao tuyến của hai mặt phẳng (MBD) và (ABN) là
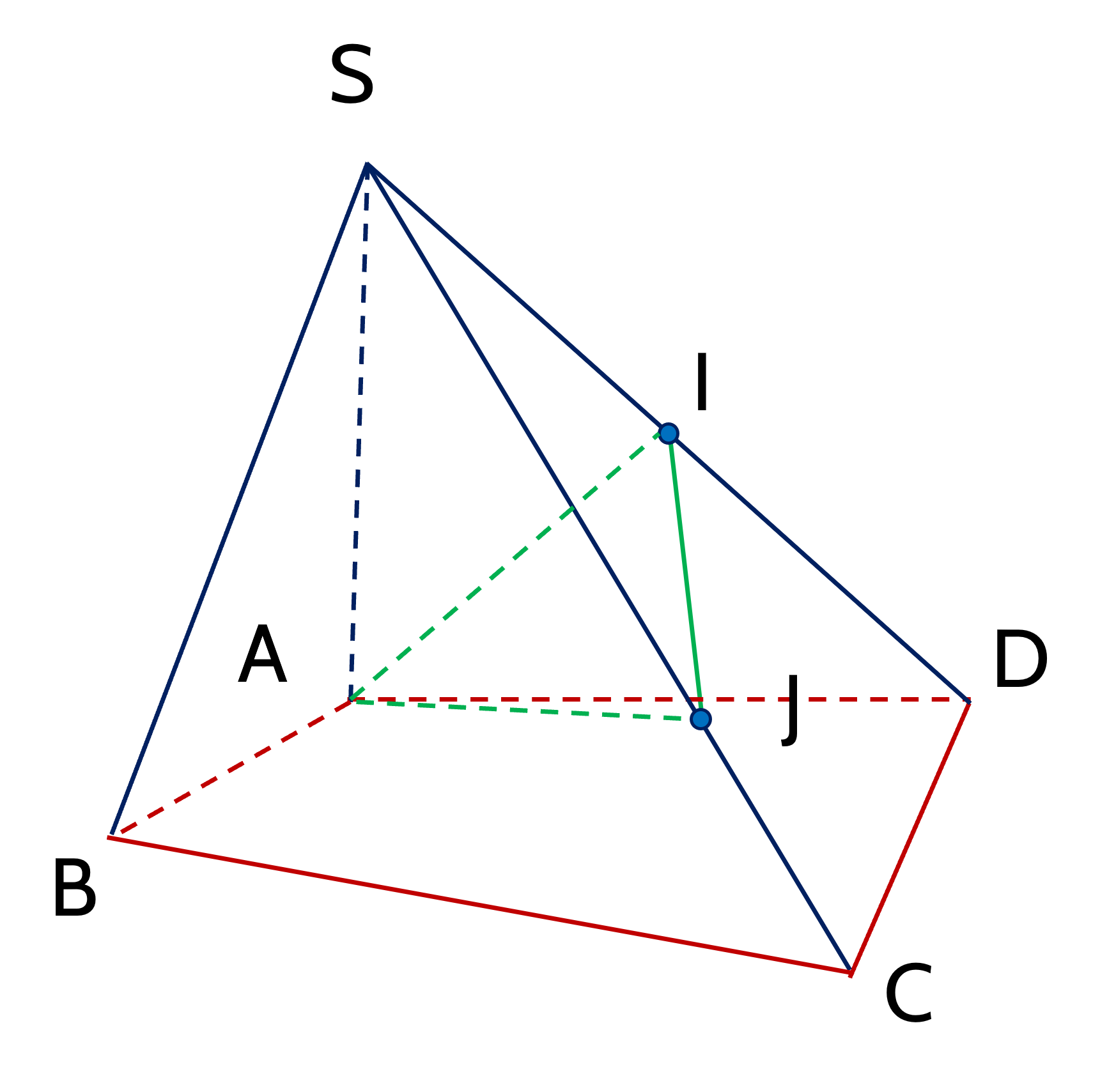
Cho hình chóp S.ABCD. Gọi I là trung điểm của SD,J là điểm trên cạnh SC và J không trùng với trung điểm SC. Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I và J lần lượt là trung điểm của SA và SB. Xét tính đúng, sai của các khẳng định sau.
(Nhấp vào dòng để chọn đúng / sai)| 1) IJCD là hình thang. |
|
| 2) (SAB)∩(IBC)=IB. |
|
| 3) (SBD)∩(JCD)=JD. |
|
| 4) (IAC)∩(JBD)=AO ( O là tâm ABCD). |
|
Cho hình chóp S.ABCD có đáy là hình thang ABCD(AD//BC). Gọi M là trung điểm CD. Giao tuyến của hai mặt phẳng (MSB) và (SAC) là


Bạn có thể đánh giá bài học này ở đây