Bài học cùng chủ đề
- Phương trình đường tròn. Phương trình tiếp tuyến của đường tròn
- Tìm tâm và bán kính dựa vào phương trình đường tròn
- Lập phương trình đường tròn (Phần 1)
- Lập phương trình đường tròn (Phần 2)
- Điều kiện để phương trình là phương trình đường tròn
- Phương trình tiếp tuyến của đường tròn
- Phương trình đường tròn đi qua ba điểm, phương trình tiếp tuyến của đường tròn
- Phương trình đường tròn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Phương trình đường tròn đi qua ba điểm, phương trình tiếp tuyến của đường tròn SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
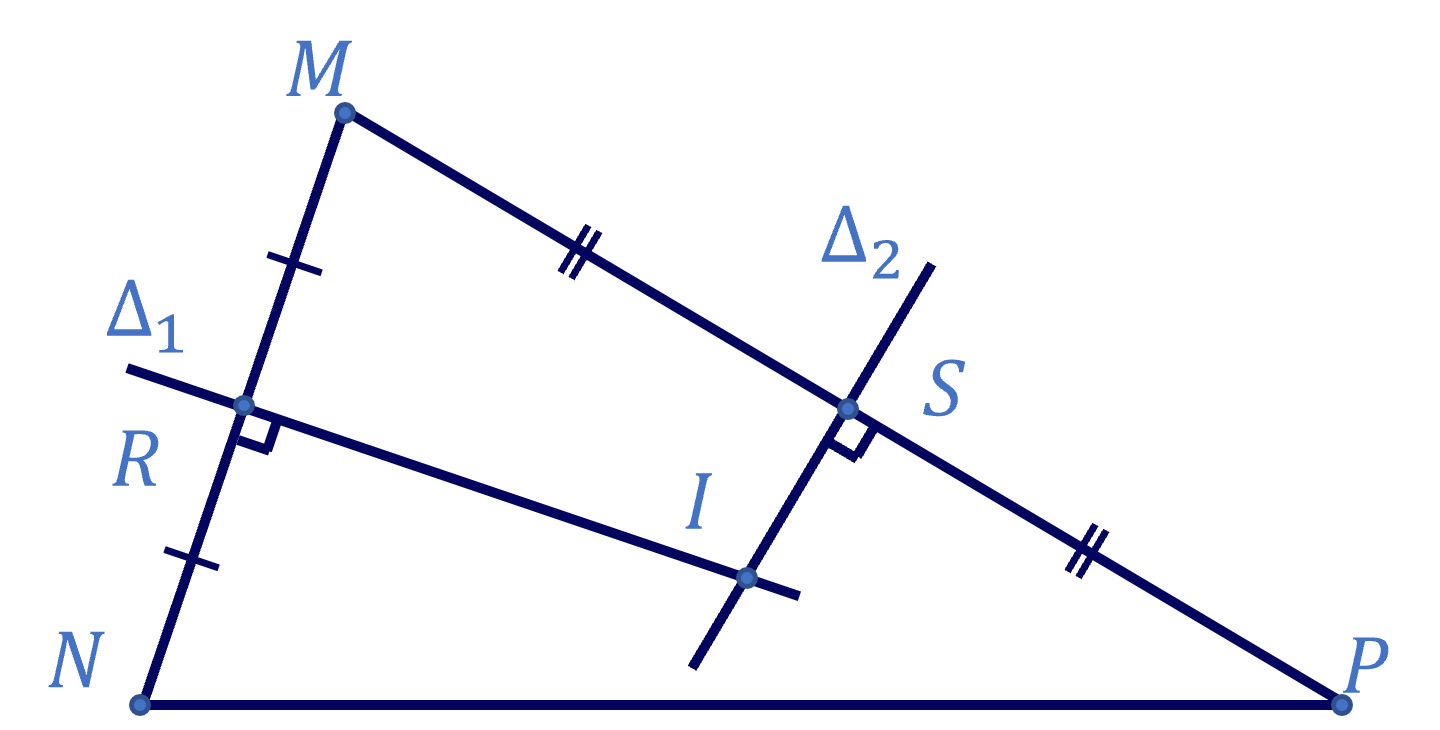
Để viết phương trình đường tròn \(\left(C\right)\) đi qua ba điểm \(M\), \(N\), \(P\). Ta viết phương trình đường trung trực \(\Delta_1\) của \(MN\), đường trung trực \(\Delta_2\) của \(MP\). Giao điểm \(I\) của \(\Delta_1\), \(\Delta_2\) là tâm đường tròn \(\left(C\right)\). Bán kính của đường tròn \(\left(C\right)\) là \(R=IM\).
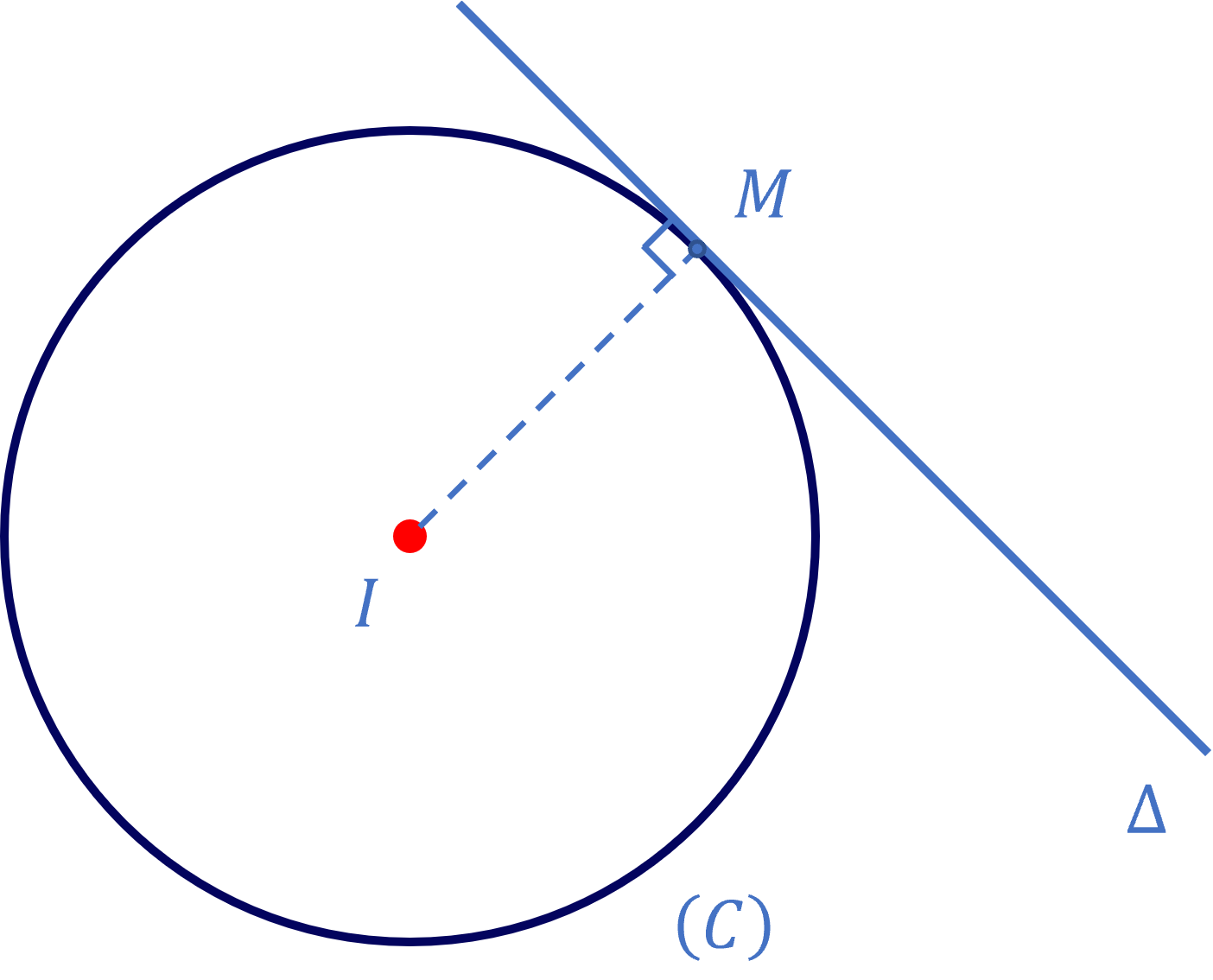
Cho điểm \(M\left(x_0;y_0\right)\) thuộc đường tròn \(\left(C\right):\left(x-a\right)^2+\left(y-b\right)^2=R^2\) (tâm \(I\left(a;b\right)\), bán kính \(R\)). Khi đó tiếp tuyến \(\Delta\) của \(\left(C\right)\) tại \(M\left(x_0;y_0\right)\) là
\(\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\).
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- ta đến với ví dụ tiếp theo Viết phương
- trình của một đường tròn thì qua 3 điểm
- cho trước
- như ta đã học để viết được phương trình
- đường tròn thì ta cần xác định được tâm
- và bán kính của đường tròn đó
- để đường tròn đi qua 3 điểm thì ba điểm
- A B C là không thẳng hàng vậy a b c tạo
- thành một tam giác
- mà đường tròn đi qua 3 điểm cùng một tam
- giác đó là đường tròn ngoại tiếp tam
- giác đường tròn ngoại tiếp tam giác thì
- có tâm là giao điểm của ba đường trung
- trực
- ta sẽ lấy đồ trên trục Delta 1 của AB và
- đường trung trực Delta 2 của AC
- dao của hai đường này đó chính là tâm I
- thẻ nhắc lại Denta 1 là đường trung trực
- của đoạn thẳng AB thì delta 1 đi qua
- trung điểm của đoạn thẳng AB lấy là điểm
- M và vuông góc với đoạn thẳng AB
- ta cần viết được phương trình của Delta
- 1 và Delta 2
- hay ta rút gọn thành 2x + y + 1 = 0
- bằng cách tương tự ta cũng biết được
- phương trình của đường thẳng delta 2
- 1/2 có một vectơ pháp tuyến là vectơ AC
- có độ là 1 -1
- và sẽ được Delta 2 có phương trình tổng
- quát là x - y - 4 = 0
- sau khi tìm được Delta 1 và Delta 2 thì
- ta lấy ra điểm của hai đường thẳng này
- và ta suy ra được tọa độ của điểm I
- là nghiệm của hệ phương trình tạo bởi
- phương trình của hai đường thẳng delta 1
- và Delta 2
- ta giải hệ phương trình này ta thu được
- x = 1 y = -3
- 1-3
- được chọn c có tâm là điểm I có một điểm
- trên đường tròn là điểm A vậy ta có thể
- lấy bán kính là
- ia
- được tính thông qua công thức đó là độ
- dài của Vectơ IA và tính của bóng 5
- vậy phương trình đường tròn C là x - 1²
- + 3² = 25
- hay là x trừ 1 Bình Phương và y trừ đi
- trừ 3
- bình phương bằng bình phương
- áp dụng ta làm một bài tập hoặc tương tự
- lập phương trình đường tròn ngoại tiếp
- tam giác có tọa độ các đỉnh là M N P cho
- cách hỏi là khác nhau Nhưng bản chất là
- giống nhau đều đã đường tròn đi qua 3
- điểm
- ta làm hoàn toàn tương tự
- RS là trung điểm của nm và MT ta cũng
- viết được Delta 1 và tuyến thứ hai là
- đường trung trực của MN và MT
- Và từ đó ta tìm được bán kính
- ta làm theo các bước để cho trực đây ta
- 1 của Mn
- pháp tuyến là vectơ MN là âm 1 âm 3 ta
- chia được phương trình của đường thẳng
- delta 1 là x + 3y - 12 = 0
- ta cũng tìm được phương trình của đường
- thẳng delta 2
- 3x - 6 = 0 sau đó ta tìm được tọa độ
- điểm I và viết được phương trình của
- hình tròn tại điểm với phần tiếp theo là
- phương trình tiếp tuyến của đường tròn
- hoạt động 2 cho đường tròn c x + 1 bình
- phương cộng y cho 2 bình phương bằng 25
- phải m 2 -2
- chứng minh điểm M 2-2 thuộc cho C
- Tâm I
- số điểm m2 -2 thuộc đường tròn C làm
- tương tự như cách chứng minh một điểm
- thuộc đường thẳng bằng cách là hết tốc
- độ
- ta thấy tốc độ điểm M và phương trình
- đường tròn c
- 2 + 1 Bình Phương cộng với lại là -2 - 2
- bình phương
- là 3 bình phương
- và bằng 25
- rồi sau đó mở thuộc cho C
- tâm và bán kính của đường tròn c ta đã
- biết phương trình đường tròn C Delta
- cũng dễ dàng Viết được tâm và bán kính
- của đường tròn c
- ta được học ở bài trước
- tâm là y -12
- bán kính r bằng căn 25 = 5
- IC gọi Delta là tiếp tuyến của C tại M
- hãy suy ra một vectơ pháp tuyến của
- đường thẳng delta từ đó Viết phương
- trình của đường thẳng delta
- tập kết luận cho điểm M x0 y0 thuộc
- đường tròn c cách tra bình phương cộng y
- trừ b bình phương bằng R bình phương khi
- đó tiếp tuyến Delta của đường tròn C tại
- M x0 y0 có vectơ pháp tuyến là vectơ Im
- có tọa độ A trừ x0 B - x0 do đó có
- phương trình tổng quát là a - x0 x0 + b
- - y0 y0
- ví dụ
- cho đường tròn c có phương trình lên
- trên và một điểm M ta phải xét xem điểm
- m này có thuộc đường tròn C hay không Và
- nếu có ta viết phương trình tiếp tuyến
- tại M của đường thẳng C
- ta làm tương tự như hoạt động vừa rồi ta
- thế tốc độ của điểm M vào phương trình
- đường tròn C xem sao
- 1 - 1 Bình Phương cộng với lại 1 + 1
- Bình Phương đó đúng bằng 4
- để với bài toán luyện tập cho đường
- thẳng C như trên Viết phương trình tiếp
- tuyến ∆ của đường tròn c tại điểm o0
- viết lại được tròn C để ta tìm được tâm
- và bán kính của đường tròn c
- ta viết lại được thành x - 4 bình phương
- cộng y trừ 3 bình phương bằng 5 Bình
- Phương từ đó ta có tọa độ của tâm I của
- đường tròn C
- là ta cũng có thể nhận thấy -8 = -2 nhân
- với 4
- -6 bằng âm 2 nhân với 3 và dễ dàng chia
- được 43 là tốc độ tâm của đường tròn C
- đường thẳng delta đi qua điểm O 0; 0
- điểm vectơ Oy là một vectơ pháp tuyến
- biên độ I là 43
- từ đây ta sẽ giảm viết được phương trình
- tổng quát của đường thẳng delta là 4x +
- 3y bằng 0
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây