Phép nhân và chia các số tự nhiên SVIP

I. PHÉP NHÂN

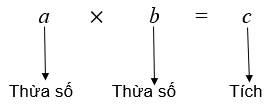
Quy ước: 

- Trong một tích, ta có thể thay thế dấu "\(\times\)" bằng dấu ".".

- Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số.

Ví dụ: \(13\times4=13.4\); \(a\times b=a.b=ab\); \(2.a.b=2ab\).

1. Nhân hai số có nhiều chữ số

Ví dụ: Tính \(152\times213\).

Ta đặt tính nhân như sau:

Vậy \(152\times213=32\) \(376\).

2. Tính chất của phép nhân

Phép nhân có các tính chất sau:

- Giao hoán:           \(a.b=b.a\);

- Kết hợp:              \(\left(a.b\right).c=a.\left(b.c\right)\);

- Nhân với số 1:     \(a.1=1.a=a\);

- Phân phối đối với phép cộng và phép trừ:

                               \(a.\left(b+c\right)=a.b+a.c\);

                               \(a.\left(b-c\right)=a.b-a.c\).

Lưu ý: 

Do tính chất kết hợp nên giá trị của biểu thức \(a.b.c\) có thể được tính theo một trong hai cách sau:

\(a.b.c=a.\left(b.c\right)\)

hoặc \(a.b.c=\left(a.b\right).c\).

Ví dụ: Tính một cách hợp lí:

a) \(25.29.4\);

b) \(37.65+37.35\).

Giải

a)     \(25.29.4\)

    \(=25.4.29\)      (tính chất giao hoán)

    \(=\left(25.4\right).29\)   (tính chất kết hợp)

    \(=100.29=2\) \(900\).

b)     \(37.65+37.35\)

    \(=37.\left(65+35\right)\)   (tính chất phân phối)

    \(=37.100=3\) \(700\).

II. PHÉP CHIA

1. Phép chia hết

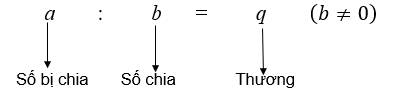
Lưu ý: 

- Nếu \(a:b=q\) thì \(a=bq\).

- Nếu \(a:b=q\) và \(q\ne0\) thì \(a:q=b\).

Ví dụ: Tính \(2\) \(795:215\).

Ta đặt tính chia như sau:

Vậy \(2\) \(795:215=13\).

2. Phép chia có dư

Cho hai số tự nhiên \(a\) và \(b\) với \(b\ne0\). Khi đó luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) sao cho \(a=b.q+r\), trong đó \(0\le r< b\).

Lưu ý: 

- Khi \(r=0\) ta có phép chia hết.

- Khi \(r\ne0\) ta có phép chia có dư. Ta nói: \(a\) chia cho \(b\) được thương là \(q\) và số dư là \(r\). Kí hiệu: \(a:b=q\) (dư \(r\)).

Ví dụ: Đặt tính để tính thương và số dư của phép chia \(2\) \(542:34\).

Giải

Ta có:

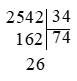
Vậy \(2\) \(542:34=74\) (dư \(26\)).