Phần tự luận (6 điểm) SVIP

Hướng dẫn giải:

Chọn chiều dương là chiều chuyển động của ô tô, gốc thời gian lúc bắt đầu hãm phanh.

Đổi 64,8 km/h = 18 m/s; 54 km/h = 15 m/s; 36 km/h = 10 m/s

a. Gia tốc của ô tô:

\(a=\dfrac{\text{v}_1-\text{v}_0}{\Delta t}=\dfrac{15-18}{10}=-0,3\) m/s²

Thời gian kể từ khi hãm phanh đến khi ô tô đạt vận tốc v₂ = 36 km/h = 10 m/s là:

\(\text{v}=\text{v}_0+at\Rightarrow t=\dfrac{\text{v}_2-\text{v}_0}{a}=\dfrac{10-18}{-0,3}=26,7\) s

b. Thời gian kể từ khi hãm phanh đến khi ô tô dừng hẳn \(\text{v}_3=0\) là:

\(t'=\dfrac{\text{v}_3-\text{v}_0}{a}=\dfrac{0-18}{-0,3}=60\) s

c. Ta có: \(\text{v}_2^2-\text{v}_0^2=2as\)

Vậy quãng đường ô tô đi được đến khi dừng hẳn là:

\(s=\dfrac{\text{v}_3^2-\text{v}_0^2}{2a}=\dfrac{0-18^2}{2\left(-0,3\right)}=540\) m

Hướng dẫn giải:

a. Vẽ đồ thị độ dịch chuyển – thời gian của Nam.

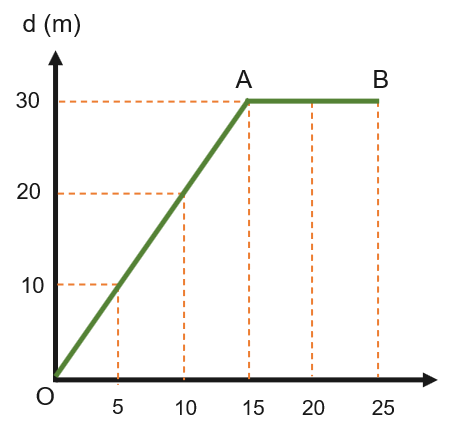
b. Mô tả chuyển động của Nam:

- Từ 0 – 15 giây: Nam chuyển động thẳng đều với vận tốc: \(\text{v}_1=\dfrac{\Delta d_1}{\Delta t_1}=\dfrac{30}{15}=2\) m/s

- Từ giây thứ 15 đến giây thứ 25: Nam đứng yên (dừng lại).

c. Vận tốc của Nam trong 15 s đầu là:

\(\text{v}_1=\dfrac{\Delta d_1}{\Delta t_1}=\dfrac{30}{15}=2\) m/s

Vận tốc của Nam trong suốt quá trình chuyển động:

\(\text{v}=\dfrac{\Delta d}{\Delta t}=\dfrac{30}{25}=1,2\) m/s

Hướng dẫn giải:

Gọi \(s\) là quãng đường viên đá đi được sau khoảng thời gian \(t\) kể từ khi bắt đầu rơi tới khi chạm đất

\(s_1\)$\mathrm{}$ là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian \(t_1=t-1\)

Ta có: \(s=\dfrac{1}{2}gt^2\) và \(s_1=\dfrac{1}{2}g\left(t-1\right)^2\)

Quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:

\(\Delta s=s-s_1=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=gt-\dfrac{1}{2}g\)

\(\Rightarrow t=\dfrac{\Delta s}{g}+\dfrac{1}{2}=\dfrac{14,7}{9,8}+\dfrac{1}{2}=2\) s