Kiểm tra cuối chương I

Câu 1 (1đ):

Khoảng cách giữa hai điểm cực trị của đồ thị hàm số $y=x^{3}-3 x^{2}+4$ bằng

2 \sqrt{5}

.

4 .

2 .

2 \sqrt{2}

.

Câu 2 (1đ):

Hàm số $y=x^{4}-2 x^{2}+1$ đồng biến trên khoảng nào dưới đây?

(-1 ;+\infty)

.

(-1 ; 0)

.

(-\infty ;-1)

.

(-3 ; 8)

.

Câu 3 (1đ):

Cho hàm số $y=\dfrac{3 x-1}{x-2}$ . Mệnh đề nào dưới đây đúng?

A

Hàm số nghịch biến trên

\mathbb{R}

.

B

Hàm số đồng biến trên các khoảng

(-\infty ; 2)

và

(2 ;+\infty)

.

C

Hàm số nghịch biến trên các khoảng

(-\infty ; 2)

và

(2 ;+\infty)

.

D

Hàm số đồng biến trên

\mathbb{R} \backslash\{2\}

.

Câu 4 (1đ):

Gọi $x_{1}$ là điểm cực đại, $x_{2}$ là điểm cực tiểu của hàm số $y=-x^{3}+3 x+2$ . Tính $x_{1}+2 x_{2}$ .

-1.

2.

1.

0 .

Câu 5 (1đ):

Giá trị lớn nhất và nhỏ nhất của hàm số $y=x^{3}-12 x+1$ trên đoạn $[-2 ; 3]$ lần lượt là

-15

và

17

.

17

và

-15

.

6

và

-26

.

10

và

-26

.

Câu 6 (1đ):

Trên đoạn $[-1 ; 2]$ , hàm số $f(x)=-x^{4}+12 x^{2}+1$ đạt giá trị lớn nhất tại

x=2.

x= 0.

x=37 .

x=33 .

Câu 7 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'(x)=x(x-1)^{2}(x-2)^{3}$ . Số điểm cực trị của hàm số $y=f(x)$ là

3 .

2 .

0 .

1 .

Câu 8 (1đ):

Tìm tiệm cận xiên của đồ thị hàm số $f(x)=\dfrac{x^{2}+3 x}{x-2}$ .

y=x+5

.

y=2 x-5

.

y=x-5

.

y=x-2

.

Câu 9 (1đ):

Giao điểm của đường tiệm cận đứng và đường tiệm cận xiên của đồ thị hàm số $y=\dfrac{2 x^{2}-3 x+2}{x-1}$ là

(1 ;-1)

.

(1 ; 1)

.

(1 ; 2)

.

(1 ; 0)

.

Câu 10 (1đ):

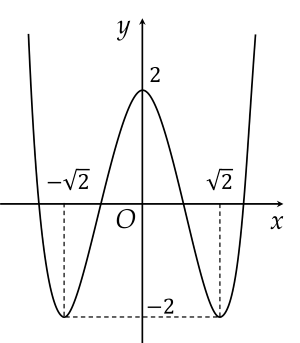
loading...

Cho hàm số $y=f(x)$ có đồ thị như hình vẽ. Hàm số $y=f(x)$ nghịch biến trên khoảng nào dưới đây?

(\sqrt{2} ;+\infty)

.

(-2 ; 2)

.

(-\infty ; 0)

.

(0 ; \sqrt{2})

.

Câu 11 (1đ):

Giá trị lớn nhất của hàm số $y=\sqrt{4-x^2}$ là

M=4

.

M=0

.

M=-2

.

M=2

.

Câu 12 (1đ):

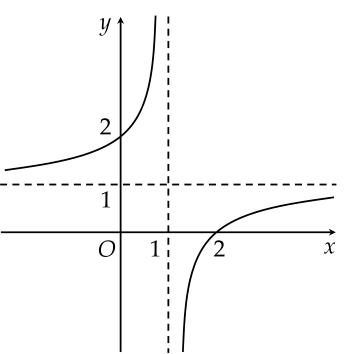
loading...

Cho hàm số $y=\dfrac{a x-b}{x+c}(a, b, c \in \mathbb{R})$ có đồ thị như hình vẽ. Giá trị của biểu thức $2 a+b-3 c$ bằng

-5 .

4 .

-3 .

7 .

Câu 13 (1đ):

Cho hàm số $f(x)=\dfrac{a x-1}{b x+c}\,(a, b, c \in \mathbb{R})$ có bảng biến thiên như hình vẽ

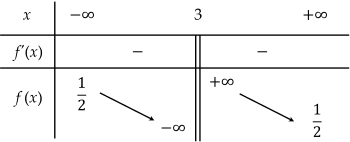
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số nghịch biến trên khoảng $\left(-\infty;\dfrac{1}{2}\right)$ .
b) Đồ thị hàm số có tiệm cận đứng $x=\dfrac{1}{2}$ .
c) Đồ thị giao với trục hoành tại điểm có hoành độ nhỏ hơn $3$ .
d) $b>\dfrac{2}{3}$ hoặc $b<0$ .

Câu 14 (1đ):

Cho đồ thị của hàm số $y=f(x)$ .

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số có $3$ điểm cực trị.
b) $\displaystyle \lim _{x \rightarrow-\infty} f(x)=2 ; \displaystyle \lim _{x \rightarrow 1^{-}} f(x)=$ $-\infty$ .
c) Đồ thị hàm số có $3$ đường tiệm cận đứng $x=-1;x=0;x=1$ .
d) Đồ thị hàm số có hai đường tiệm cận ngang $y=2$ và $y=0$ .

Câu 15 (1đ):

Cho hàm số $f(x)=\dfrac{x^2+4 x+5}{x+2}$ . Khi đó

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số có tập xác định: ${D}=(-\infty ;-2) \cap (-2 ;+\infty)$ .
b) Vì $\displaystyle \lim _{x \rightarrow+\infty} f(x)=\displaystyle \lim _{x \rightarrow+\infty}\left(x+2+\frac{1}{x+2}\right)=+\infty$ nên hàm số có tiệm cận xiên là đường thẳng $y=x+2$ .
c) Vì $\displaystyle \lim _{x \rightarrow-2^{+}} f(x)=\displaystyle \lim _{x \rightarrow-2^{+}} \frac{x^2+4 x+5}{x+2}=+\infty$ nên đường thẳng $x=-2$ là tiệm cận đứng của đồ thị hàm số.
d) Đồ thị hàm số nhận $I(-2 ; 0)$ làm tâm đối xứng.

Câu 16 (1đ):

Xét phản ứng hóa học tạo ra chất $C$ từ hai chất $A$ và $B: A+B \longrightarrow C$ . Giả sử nồng độ của hai chất $A$ và $B$ bằng nhau $[A]=[B]=a({~mol} / {l})$ . Khi đó, nồng độ của chất $C$ theo thời gian $t$ $(t>0)$ được cho bởi công thức: $[C]=\dfrac{a^2 K t}{a K t+1}({~mol} / {l})$ , trong đó $K$ là hằng số dương.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nồng độ của chất $C$ tại thời điểm $t=2$ là $\dfrac{2a^2K }{2aK +1}$ $({~mol} / {l})$ .
b) Công thức biểu thị tốc độ phản ứng tại thời điểm $t>0$ là $\dfrac{a^2Kt}{aKt+1}$ .
c) Khi $t \rightarrow +\infty$ thì $[C] \rightarrow +\infty$ .
d) Khi $t \rightarrow +\infty$ thì $[C]'(t) \rightarrow 0$ .

Câu 17 (1đ):

Cho hàm số $f(x)=2 x^3-3 x^2+m$ thoả mãn $\underset{ [0;5] }{{\min}}f(x)=5$ . Khi đó giá trị của $m$ bằng bao nhiêu?

Trả lời: .

Câu 18 (1đ):

Biết đồ thị $(C)$ của hàm số $y=\dfrac{x^2-4 x+5}{x-1}$ có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $(C)$ tạo với hai trục tọa độ một tam giác có diện tích $S$ bằng bao nhiêu?

Trả lời: .

Câu 19 (1đ):

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=\sin ^3 x-3 \sin ^2 x+2$ lần lượt là $M, m$ . Tổng $M+m$ bằng bao nhiêu?

Trả lời: .

Câu 20 (1đ):

Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số $N(t)=-t^3+12 t^2, 0 \leq t \leq 12$ , trong đó $N$ là số người bị nhiễm bệnh (tính bằng trăm người) và $t$ là thời gian (tuần). Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.

Trả lời: .

Câu 21 (1đ):

Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích $1$ lít. Tìm chiều cao của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất (Kết quả được tính theo centimét và làm tròn đến chữ số thập phân thứ hai).

Trả lời: cm.

Câu 22 (1đ):

Để loại bỏ $p \%$ một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là $C(p)=\dfrac{45 p}{100-p}$ (triệu đồng), với $0 \leq p <100.$ Biết rằng tiệm cận đứng của đồ thị hàm số $C(p)$ có dạng $p=a$ . Khi đó $a$ bằng bao nhiêu?
Trả lời: .

Bài học cùng chủ đề

Kiểm tra cuối chương I SVIP

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Kiểm tra cuối chương I SVIP

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP