Bài học cùng chủ đề
- Lũy thừa với số mũ tự nhiên
- Luỹ thừa với số mũ tự nhiên
- Tích và thương hai luỹ thừa cùng cơ số
- Luỹ thừa của luỹ thừa
- Luỹ thừa số hữu tỉ với số mũ tự nhiên (Phần 1)
- Luỹ thừa số hữu tỉ với số mũ tự nhiên (Phần 2)
- (Em có biết) Luỹ thừa một tích, luỹ thừa một thương
- (Em có biết) Luỹ thừa với số mũ âm
- Phiếu bài tập: Lũy thừa với số mũ tự nhiên của số hữu tỉ
- Lũy thừa với số mũ tự nhiên của một số hữu tỉ
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lũy thừa với số mũ tự nhiên SVIP
1. LŨY THỪA VỚI SỐ MŨ TỰ NHIÊN
Lũy thừa bậc \(n\) của một số hữu tỉ \(x\), kí hiệu \(x^n\), là tích của \(n\) thừa số \(x\) (\(n\) là số tự nhiên lớn hơn 1):
\(x^n\) đọc là \(x\) mũ \(n\) hoặc \(x\) lũy thừa \(n\) hoặc lũy thừa bậc \(n\) của \(x\).
\(x\) gọi là cơ số, \(n\) gọi là số mũ.
Quy ước: \(x^0=1\left(x\ne0\right);x^1=x\).
Ví dụ: Tính: \(\left(\dfrac{-2}{3}\right)^3\).
Giải
\(\left(\dfrac{-2}{3}\right)^3=\dfrac{-2}{3}.\dfrac{-2}{3}.\dfrac{-2}{3}=\dfrac{\left(-2\right).\left(-2\right).\left(-2\right)}{3.3.3}=\dfrac{-8}{27}\).
Ví dụ: Tính:
a) \(\left(\dfrac{1}{2}\right)^2.2^2\);
b) \(\dfrac{\left(-6\right)^3}{2^3}\).
Giải
a) \(\left(\dfrac{1}{2}\right)^2.2^2=\left(\dfrac{1}{2}.\dfrac{1}{2}\right).\left(2.2\right)=\left(\dfrac{1}{2}.2\right).\left(\dfrac{1}{2}.2\right)=\left(\dfrac{1}{2}.2\right)^2=1^2=1\).
b) \(\dfrac{\left(-6\right)^3}{2^3}=\dfrac{\left(-6\right).\left(-6\right).\left(-6\right)}{2.2.2}=\left(\dfrac{-6}{2}\right)^3=\left(-3\right)^3=-27\).
Chú ý: Lũy thừa của một tích bằng tích các lũy thừa;
Lũy thừa của một thương bằng thương các lũy thừa.
2. TÍCH VÀ THƯƠNG HAI LŨY THỪA CÙNG CƠ SỐ
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.
\(x^m.x^n=x^{m+n}\).
Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.
\(x^m:x^n=x^{m-n}\left(x\ne0,m\ge n\right)\).
Ví dụ: Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:
a) \(\left(-\dfrac{5}{7}\right)^3.\left(-\dfrac{5}{7}\right)^2\);
b) \(\left(-0,4\right)^6:\left(-0,4\right)^3\).
Giải
a) \(\left(-\dfrac{5}{7}\right)^3.\left(-\dfrac{5}{7}\right)^2=\left(-\dfrac{5}{7}\right)^{3+2}=\left(-\dfrac{5}{7}\right)^5\).
b) \(\left(-0,4\right)^6:\left(-0,4\right)^3=\left(-0,4\right)^{6-3}=\left(-0,4\right)^3\).
3. LŨY THỪA CỦA LŨY THỪA
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.
\(\left(x^m\right)^n=x^{m.n}\).
Ví dụ: Viết \(2^{15}\) dưới dạng lũy thừa của 8.
Giải
\(2^{15}=2^{3.5}=\left(2^3\right)^5=8^5\).

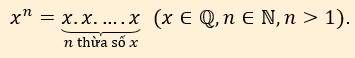
Bạn có thể đánh giá bài học này ở đây