Bài học cùng chủ đề
- Đường thẳng song song với mặt phẳng
- Một số dạng toán về đường thẳng song song với mặt phẳng
- Đường thẳng song song với mặt phẳng
- Tìm thiết diện của mặt phẳng với khối chóp
- Bài tập mẫu: Chứng minh đường thẳng song song với mặt phẳng
- Bài tập mẫu: Dựng mặt phẳng song song với đường thẳng
- Bài tập mẫu: Thiết diện
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đường thẳng song song với mặt phẳng SVIP
1. Đường thẳng song song với mặt phẳng
a) Định nghĩa:
Cho đường thẳng $d$ và mặt phẳng $(\alpha)$. Nếu $d$ và $(\alpha)$ không có điểm chung thì ta nói $d$ song song với $(\alpha)$ hay $(\alpha)$ song song với $d$ và kí hiệu là $d//(\alpha)$ hay $(\alpha)//d$.
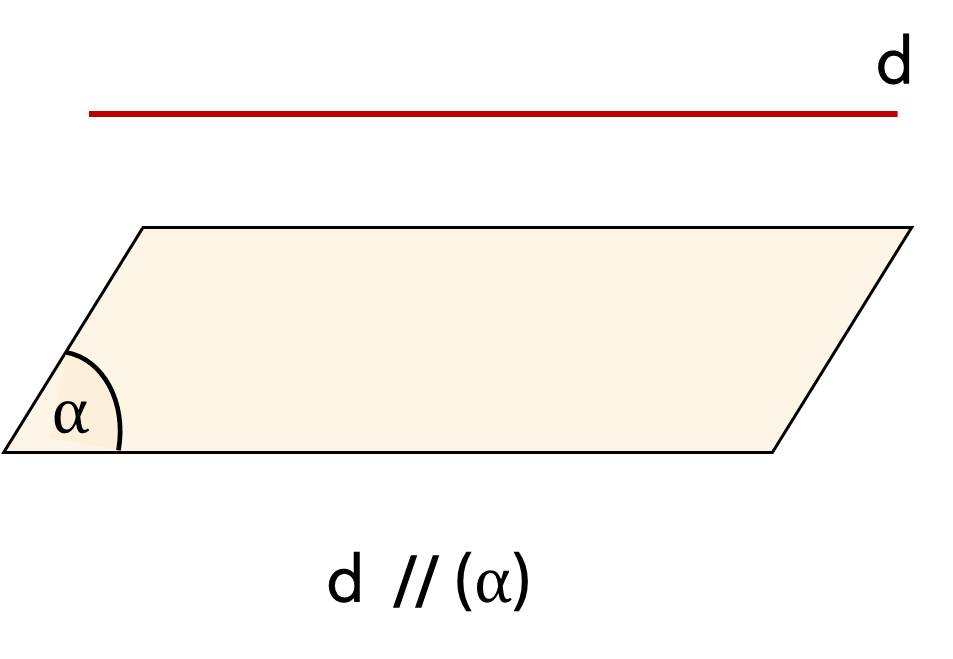
* Chú ý:
+ Nếu $d$ và $(\alpha)$ có một điểm chung duy nhất $M$ thì ta nói $d$ và $(\alpha)$ cắt nhau tại điểm $M$ và kí hiệu $d \cap(\alpha)=\{M\}$ hay $d \cap(\alpha)=M$.
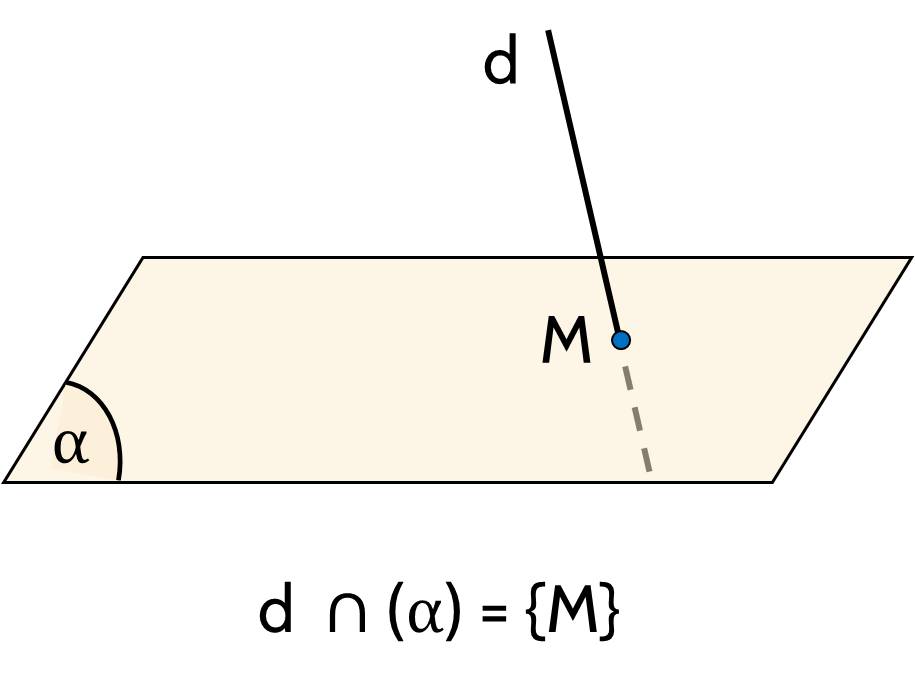
+ Nếu $d$ và $(\alpha)$ có nhiều hơn một điểm chung thì ta nói $d$ nằm trong $(\alpha)$ hay $(\alpha)$ chứa $d$ và kí hiệu $d \subset(\alpha)$ hay $(\alpha) \supset d$.
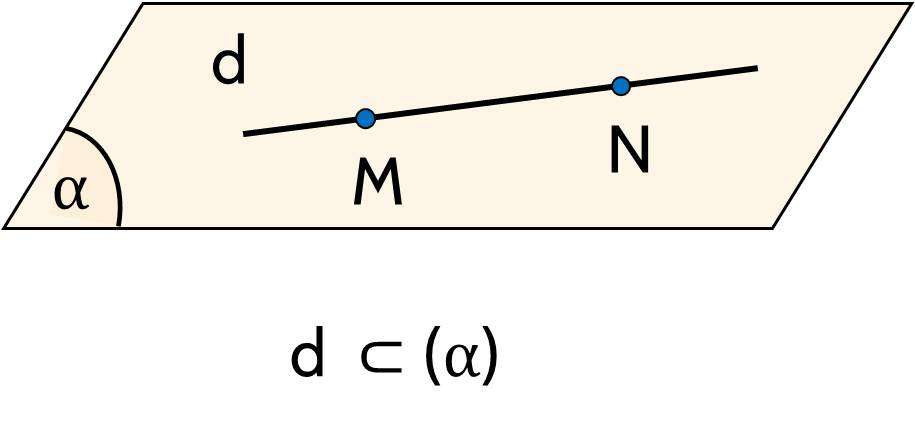
b) Luyện tập
2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng
a) Điều kiện
Nếu đường thẳng $a$ không nằm trong mặt phẳng $(P)$ và song song với một đường thẳng nằm trong $(P)$ thì a song song với $(P)$.
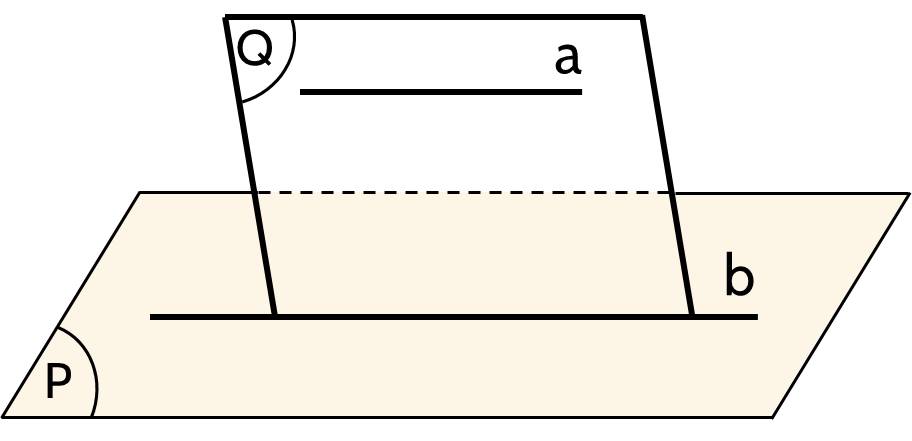
Kí hiệu: $\left\{\begin{aligned}& a \not\subset (P) \\& b \subset (P) \\& a//b \end{aligned}\right. \Rightarrow a // (P)$.
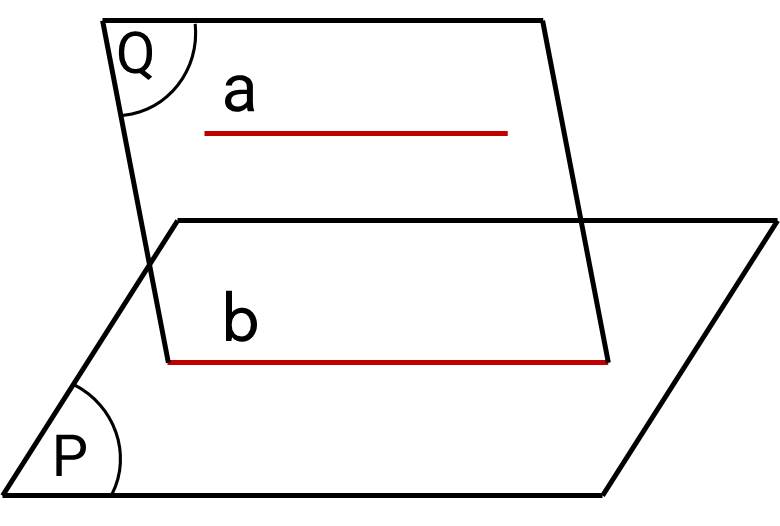
Mệnh đề: Trong không gian cho hai đường thẳng chéo nhau a và b, tồn tại một mặt phẳng chứa a và song song với b.
Chứng minh:
Hình vẽ minh hoạ:
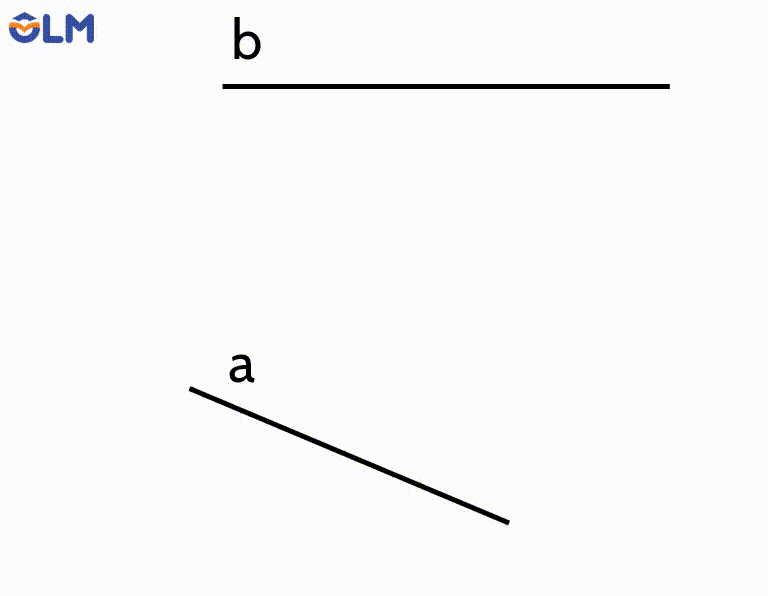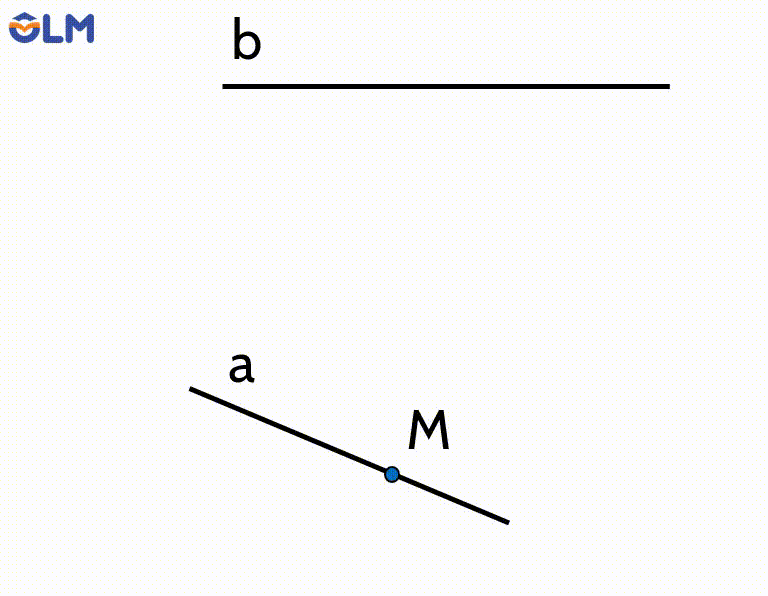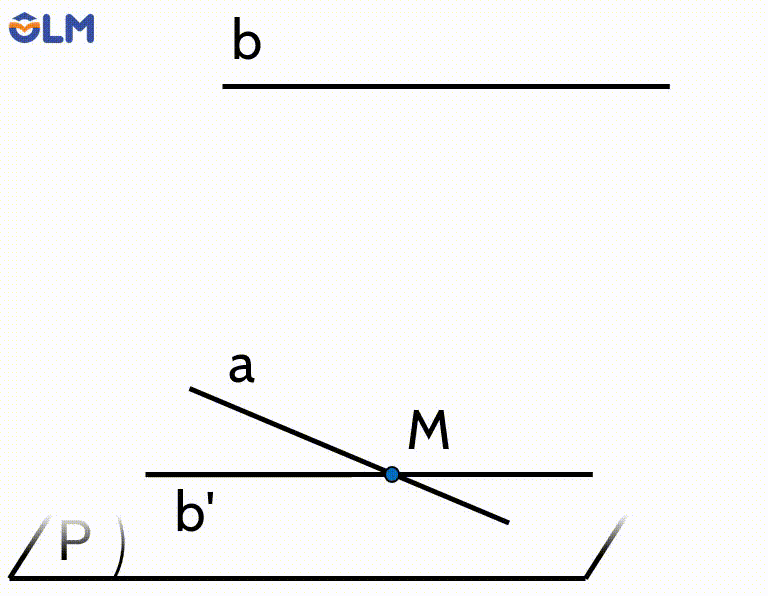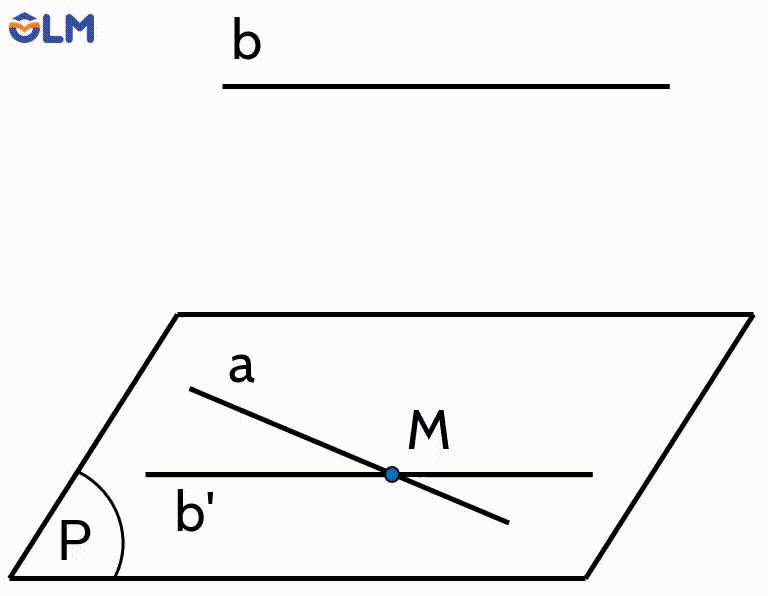
Lấy điểm $M$ bất kì thuộc $a$. Qua $M$ kẻ đường thẳng $b^{\prime}$ song song với $b$ và đặt $(P)=\mathrm{mp}\left(a, b^{\prime}\right)$.
Vì $a$ và $b$ chéo nhau nên đường thẳng $b$ không nằm trong mặt phẳng $(P)$. Vì $b$ song song với $b$ ' nằm trong mặt phẳng $(P)$ nên $b$ song song với $(P)$. Vậy $(P)$ là mặt phẳng chứa $a$ và song song với $b$.
b) Tính chất
Cho đường thẳng a song song với mặt phẳng $(P)$. Nếu mặt phẳng $(Q)$ chứa a và cắt $(P)$ theo giao tuyến $b$ thì $b$ song song với $a$.

Bạn có thể đánh giá bài học này ở đây