Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) Áp dụng quy tắc dấu ngoặc ta có:

$(2022 + 169) - (2022 - 31) = 2022 + 169 - 2022 + 31$

$= (2022 - 2022) + (169 + 31)$ (Thay đổi vị trí các số hạng kèm theo dấu và nhóm các số hạng)

$=0 + 200 = 200$.

b) $(-25)(4 - 40) + 2022^0 = (-25)[4 + (-40)] + 1$ (vì trừ đi một số là cộng với số đối của số đó và vì $2022^0 = 1$)

$=(-25).4 + (-25) . (-40) + 1 = -100 + 1000 + 1$

$= (1000 - 100) + 1 = 901$.

Hướng dẫn giải:

a) $(-5)x - 2^2 = -3^2$ hay $(-5)x - 4 = -9$

Suy ra $(-5)x = -9 + 2 = -5$.

Do đó $x = (-5) \, : \, (-5) = 1$.

b) $(-75) \, : \, (x + 6) = -15$ hay $(x + 6) = (-75) \, : \, (-15) = 5$

Suy ra $x = 5-6 = -1$.

Hướng dẫn giải:

Sau khi phát sáng lần đầu bóng, bóng đèn thứ nhất phát sáng vào các giây thứ 6 ; 12 ; 18 ;… (các bội của 6).

Tương tự, sau lần phát sáng đầu tiên, bóng đèn thứ hai phát sáng vào các giây thứ 8 ; 16 ; 24 ;… (các bội của 8).

Thời gian phát sáng của bóng thứ ba vào các giây thứ 10 ; 20 ; 30 ;…(các bội của 10).

Sau lần phát sáng đầu, cả ba bóng sẽ cùng phát sáng lần tiếp theo đầu tiên vào giây thứ là bội số chung nhỏ nhất của 6 ; 8 và 10.

Phân tích ra thừa số nguyên tố:

6 = 2.3;   8 = 2$^3$;   10 = 2.5

BCNN(6 , 8 , 10) = 2$^3$.3.5 = 120.

Vậy sau lần phát sáng đầu, ba bóng sẽ cùng phát sáng lần tiếp theo đầu tiên vào giây thứ 120.

Hướng dẫn giải:

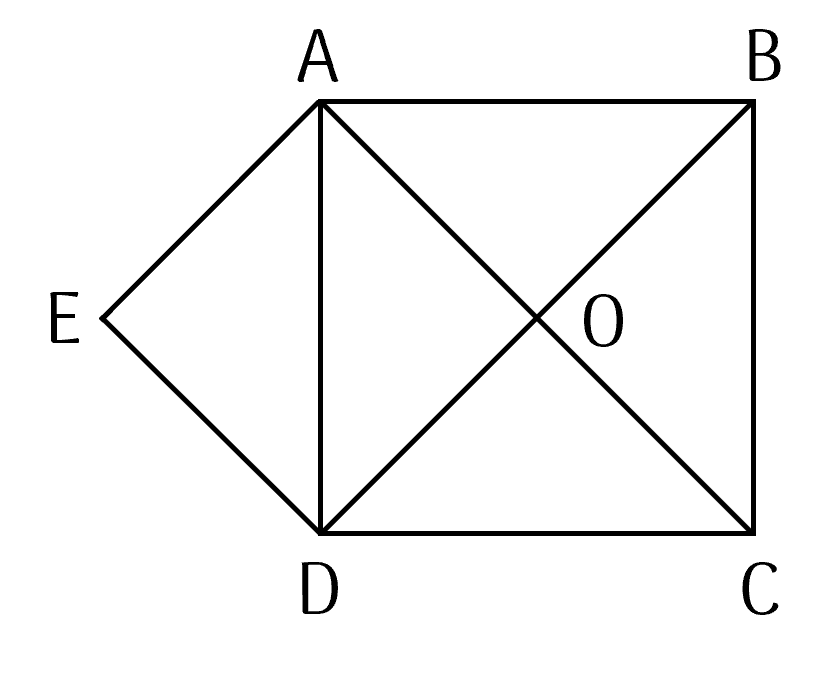
c) Hình vuông ABCD có diện tích bằng 2.2 = 4 cm$^2$.

Hai đường chéo của hình vuông ABCD chia hình vuông thành tam giác có diện tích bằng nhau, mỗi tam giác có diện tích bằng 4 : 4 = 1 cm$^2$.

Diện tích tam giác AED = diện tích tam giác AOD = 1 cm$^2$.

Diện tích hình ABCDE là 4 + 1 = 5 cm$^2$.

Hướng dẫn giải:

$311$ cọc là các đầu mút của $310$ đoạn thẳng liên tiếp (hai đoạn cạnh nhau có một đầu mút chung), mỗi đoạn dài $1,5$ m.

Tổng chiều dài của $310$ đoạn thẳng đó bằng $310 . 1,5 = 465$ m.

Kể cả $3$ mét làm lối ra vào, chu vi khu đất hình chữ nhật đó là $465 + 3 = 468$ m.

Nửa chu vi hình chữ nhật bằng $468$ $:$ $2 = 234$ m.

Chiều rộng hình chữ nhật bằng:

$234.5 \, : \, (5+8) = 90$ m.

Chiều dài hình chữ nhật bằng:

$234 - 90 = 144$ m.

Diện tích khu đất là $144.90 = 12 \, 960$ m$^2$.

Sản lượng rau thu được từ khu đất đó là $12 \, 960.5 = 64 \, 800$ kg.

Đổi sang đơn vị tạ : $64$ $800$ kg = $648$ tạ.