Bài học cùng chủ đề
Đề thi thử học kì I lớp 8 (đề số 2) SVIP
Câu 1. (2 điểm): Tính (thu gọn).
a) $(6 x-7)(7 x-1)$;
b) $(4 x-1)^2+(2 x-5)(2 x+5)$;
c) $\dfrac{x+5}{x}+\dfrac{x}{x-5}+\dfrac{25}{x^2-5 x}$.
Câu 2. (2 điểm): Phân tích đa thức thành nhân tử.
a) $5 x^2-10 x$;
b) $x^2-y^2-2 x+2 y$;
c) $x^2+10 x-y^2+25$.
Câu 3. (1,5 điểm): Tìm $x$, biết:
a) $(x+2)^2-x(x-1)=10$;
b) $x^3-6 x^2+9 x=0$.
Câu 4. (1 điểm):
Một chiếc xe đạp điện giá 12 000 000 đồng. Cửa hàng mới khai trương nên giảm giá 10%. Anh Nam tới mua chiếc xe vì anh nhận được 1 voucher giảm giá thêm 8% trên giá đã giảm. Vậy anh Nam cần trả bao nhiêu để mua chiếc xe?
Câu 5. (1 điểm):
Tầng trệt của một căn phòng có dạng hình thang với hai đáy $AB$ và $CD$, người ta muốn làm thêm một chiếc rèm ở chính giữa với một thanh sắt ngang $E F$ sao cho $E$ và $F$ lần lượt là trung điểm của $A D$ và $B C$ (như hình vẽ).
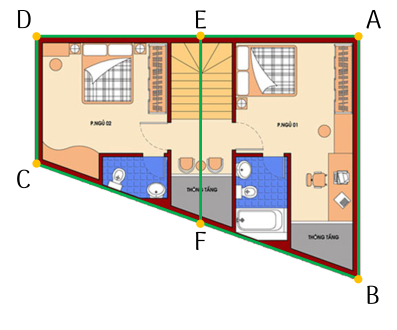
Biết $A B=8$ m, $CD=5$ m. Tính $E F$.
Câu 6. (2,5 điểm): Cho tam giác $A B C$ vuông tại $A$, $(A B<A C)$. Gọi $E$ là trung điểm của $B C$. Từ $E$ lần lượt kẻ $E D$ vuông góc với $A C$ tại $D$, $E F$ vuông góc với $A B$ tại $F$.
a) Chứng minh tứ giác $A D E F$ là hình chữ nhật;
b) Gọi $K$ là điểm đối xứng của $E$ qua $F$. Chứng minh tứ giác $A E B K$ là hình thoi;
c) Qua $D$ vẽ đường thẳng vuông góc với $B C$ cắt $A B$ tại $M$. Đường thẳng vuông góc với $A C$ tại $C$ cắt $M D$ tại I. Chứng minh tứ giác $M C I A$ là hình bình hành.
