Question

[Cao Minh Phúc]

1) cho góc xOy có Oz là tia phân giác , M là điểm bất kì thuộc tia Oz . qua M kẻ đường thẳng a vuông góc với Ox tại A cắt Oy tại C và vẽ đường thẳng b vuông góc Oy tại B cắt tia Ox tại D

a) chứng minh tam giác AOM bằng tam giác BOM từ đó suy ra OM là đường trung trực  của đoạn thẳng AB

b) tam giác DMC là tam giác jk ? vì sao ?

2) cho tam giác ABC có góc A = 90 và đường phận giác BH ( H thuộc AC ) kẻ HM vuông góc với BC ( M thuộc BC ) gọi N là gia điểm của AB và MH chúng minh

a) tam giác ABH bằng tam giác MBH

b) BH là đương trung trực cyar đoạn thẳng AM

c) AM//CN

d) BH vuông góc với CN

3) cho tam giác ABC vuông tại C có góc A = 60 và đường phân giác cua góc BAC cắt BC tại E kẻ EK vuông góc với AB tại K ( K thuộc AB ) kẻ BD vuông góc với AE tại D ( D thuộc AE ) chứng minh

a) tam giác ACE bằng tam giác AKE

b)AE là đường trung trực của đoạn thẳng CK

c) KA=KB

4) cho tam giác ABC có góc A = 90 vẽ phân giác BD và CE ( D thuộc ac , E thuộc AB ) chúng cắt nhau tại O

a) tính số đo góc BOC

b) trên BC lấy M,N sao cho BM=BA, CN=CA chứng minh EN//DM

c) gọi I là giao điểm của BD VÀ AN . chứng minh tam giác AIM vuông cân

5) cho tam giác ABC ( AB=AC ) gọi K là trung điểm của BC

a) chứng minh tam giác AKB tam giác AKC và AK vuông góc với BC

b) từ C vẽ đường vuông góc với BC cắt đường thẳng AB tại E chúng minh EC //AK

c) tam giác BCE là tam giác jk ? tính góc BEC

6) cho tam giác ABC biết AB < BC trên tia BA lấy điểm D sao cho BC= BD nối C với D . phân giác góc B cắt cạn AC , DC lần lượt ở E và I 

a) chứng minh tam giác BED = tam giác BEC và IC=ID

b) từ A vẽ đường vuông góc AH với DC ( H thuộc DC ) . chứng minh AH//BL

       VẼ HÌNH VÀ GIẢI CHI TIẾT CÁC BAI HỘ MÌNH NHA

Answer 1

[Huy Hoàng]

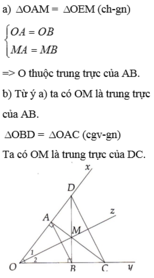
3/ (Bạn tự vẽ hình giùm. Vẽ hình dễ)

a/ \(\Delta ACE\)vuông và \(\Delta AKE\)vuông có: \(\widehat{CAE}=\widehat{EAK}\)(AE là đường phân giác của \(\Delta ABC\))

Cạnh huyền AE chung

=> \(\Delta ACE\)vuông = \(\Delta AKE\)vuông (cạnh huyền - góc nhọn) (đpcm)

b/ Ta có \(\Delta ACE\)= \(\Delta AKE\)(cm câu a) => AC = AK (hai cạnh tương ứng)

Gọi M là giao điểm của AE và CK.

\(\Delta ACM\)và \(\Delta AKM\)có: AC = AK (cmt)

\(\widehat{CAM}=\widehat{MAK}\)(AM là đường phân giác của \(\Delta ABC\))

Cạnh AM chung

=> \(\Delta ACM\)= \(\Delta AKM\)(c - g - c) => CM = KM (hai cạnh tương ứng) (1)

và\(\widehat{AMC}=\widehat{AMK}\)(hai góc tương ứng)

Mà \(\widehat{AMC}+\widehat{AMK}\)= 180^o (kề bù)

=> 2\(\widehat{AMC}\)= 180^o

=> \(\widehat{AMC}\)= 90^o

=> AM \(\perp\)CK (2)

Từ (1) và (2) => AE là đường trung trực của CK (đpcm)

Answer 2

[Cao Minh Phúc]

tsk nha