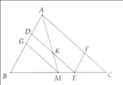
Cho AM là trung tuyến của ∆ABC. Lấy điểm I thuộc BM, kẻ đường thẳng đi qua I và song song với AB cắt AM, AC thứ tự tại D, E. Đường thẳng đi qua I và song song với AC cắt AB tại K. Chứng minh rằng: BK= DE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
15 tháng 4 2021
Lời giải:
a) Áp dụng định lý Talet cho:
Tam giác $CFD$ có $AM\parallel FD$:
$\frac{DF}{AM}=\frac{CD}{CM}(1)$
Tam giác $ABM$ có $ED\parallel AM$:
$\frac{ED}{AM}=\frac{BD}{BM}(2)$
Lấy $(1)+(2)\Rightarrow \frac{DE+DF}{AM}=\frac{CD}{BC:2}+\frac{BD}{BC:2}=\frac{BC}{BC:2}=2$
$\Rightarrow DE+DF=2AM$
Vì $AM$ không đổi khi $D$ di động nên $DE+DF$ không đổi khi $D$ di động
b) Dễ thấy $KADM$ là hình bình hành do có các cặp cạnh đối song song. Do đó $KA=DM$
Áp dụng định lý Talet cho trường hợp $AK\parallel BD$:
$\frac{KE}{ED}=\frac{KA}{BD}=\frac{DM}{BD}(3)$
Lấy $(1):(2)$ suy ra $\frac{DF}{ED}=\frac{CD}{BD}$
$\Rightarrow \frac{EF}{ED}=\frac{CD}{BD}-1=\frac{CD-BD}{BD}=\frac{CM+DM-(BM-DM)}{BD}=\frac{2DM}{BD}(4)$
Từ $(3);(4)\Rightarrow \frac{2KE}{ED}=\frac{EF}{ED}$
$\Rightarrow 2KE=EF\Rightarrow FK=EK$ hay $K$ là trung điểm $EF$
K
30 tháng 3 2020
Qua K vẽ đường thẳng // với AB cắt AC tại H.
=> AHKD là hình bình hành => DK = AH (1)
Gọi giao điểm của AK và DH là O. Vì AHKD là HBH => DO = OH
Xét 3 đường thẳng MA, CA, BA đồng quy tại A cắt 2 đường thẳng DH và BC ta được: DO/OH = BM/MC = 1
=> DH // BC (định lí chùm đường thẳng đồng quy đảo)
Xét ∆ ADH và ∆ FEC có:
AD = EF ( t/c đoạn chắn) ; DH = EC (t/c đoạn chắn) ; ^ADH = ^FEC => ∆ ADH = ∆ FEC (c-g-c)
=> AH = CF (2)
Từ (1) và (2) => CF = DK (đpcm)
GL
31 tháng 3 2020
Do EF//AB⇒\(\frac{CF}{CA}=\frac{EF}{AB}\)⇒\(\frac{CF}{EF}=\frac{AC}{AB}\)(1)
Dựng MG//AC và MM là trung điểm cạnh BC
⇒GM là đường trung bình ΔABC
=⇒G là trung điểm cạnh AB ⇒AG=BG
Do DK//GM⇒\(\frac{AD}{AG}=\frac{DK}{GM}\)⇒\(\frac{AD}{BG}=\frac{DK}{GM}\)
=> \(\frac{DK}{AD}=\frac{GM}{BG}=\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB}\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\frac{CF}{EF}=\frac{DK}{AD}\)
Mà tứ giác ADEF là hình bình hành (vì EF//AD và DE//AF) nên AD=EF
=> CF=DK (đpcm)
Nguồn: thuynga
bon cui