Một lớp học gồm 23 nữ và 17 nam. Các học sinh này đứng một cách ngẫu nhiên thành hai hàng ngang, mỗi hàng 20 người, mỗi người ở hàng này đối diện với một người ở hàng kia. Sau dó, từng cặp đối diện bắt tay nhau. Chứng minh rằng, dù đứng thế nào, số lần bắt tay giữa hai bạn nữ luôn nhiều hơn số lần bắt tay đúng 3 cái.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Xếp 12 học sinh thành 1 dãy có: 12! Cách sắp xếp.
Chọn 2 bạn nữ và sắp xếp 2 bạn đứng đầu hàng và cuối hàng có: 2 . C 7 2 cách.
Sắp xếp 10 bạn còn lại có: 10! Cách.
Do đó có: 2 C 7 2 . 10 ! cách sắp xếp 12 học sinh sao cho người đứng đầu hàng và cuối hàng đều là nữ.
Xác suất cần tìm là: P = 2 . C 7 2 . 10 ! 12 ! = 7 22

Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
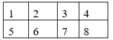
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
![]()

Xếp Phúc Đức cạnh nhau có \(2!\) cách
Xếp 4 học sinh nữ có \(4!\) cách
4 học sinh nữ tạo ra 5 khe trống, xếp cặp Phúc-Đức và 3 học sinh nam còn lại vào 5 khe trống này có: \(A_5^4\) cách
\(\Rightarrow2!.4!.A_5^4\) cách xếp thỏa mãn

Chọn C
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố "không có hai học sinh nữ nào đứng cạnh nhau".
Mỗi phần tử của A tương ứng với 1 hàng ngang gồm 11 bạn đã cho mà không có hai nữ xếp cạnh nhau. Để xếp được 1 hàng như vậy ta thực hiện liên tiếp hai bước:
Bước 1: Xếp 6 bạn nam thành một hàng ngang, có 6!= 720 cách
Bước 2: Xếp 5 bạn nữ vào 7 vị trí xen giữa hai nam hoặc ngoài cùng (để 2 nữ không cạnh nhau), có A 7 5 = 2520 cách.
Vậy n(A) =720.2520 = 1814400
Xác suất cần tìm là 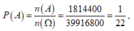

a: Coi 3 bạn nữ như 1 người
Số cách xếp là:
\(8!\cdot3!\)(cách)
b: Số cách xếp là:
\(10!-8!\cdot3!\left(cách\right)\)
