Cho tam giác ABC các trung tuyến BM;CN cắt nhau tại G gọi P là điểm đối xứng của M qua G ;gọi Q là điểm đối xứng của N qua G
tứ giác MNPQ la hình gì ?
NẾU tam giác ABC cân ở A thì tứ giác MNPQ là hình gì ?vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 5 2023
Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
14 tháng 5 2023
Mình xin phép sửa đề:
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)
8 tháng 11 2021
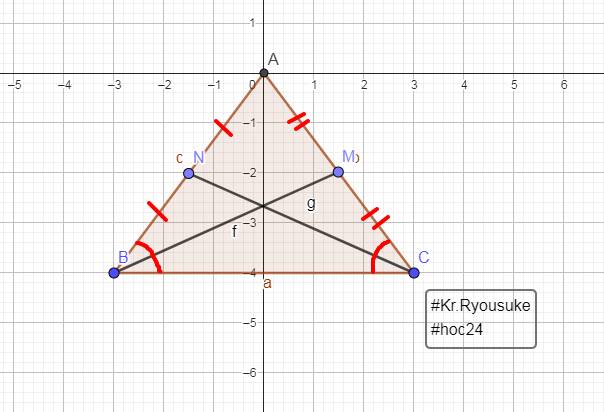
a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: \(MN=\dfrac{BC}{2}=5\left(cm\right)\)
BC
0
H9
HT.Phong (9A5)
CTVHS
23 tháng 3 2023
Do \(BM\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AM=CM\)
Và \(CN\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AN=BN\)
Mà \(BM=CN\left(gt\right)\)
Từ đó suy ra: \(AM=CM=AN=BN\)
Ta lại có: \(AM+CM=AC\)
Và \(AN+BN=AB\)
Nên: \(AM=CM=AN=BN\)
\(\Rightarrow AM+CM=AN+BN\)
\(\Rightarrow AC=AB\)
Vậy \(\Delta ABC\) có \(AC=AB\) là tam giác cân tại \(A\)
LG
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G .Cho biết NBC < MBC .Chứng minh BM
3
8 tháng 3 2023
a: Xet ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
=>ΔAHB=ΔAHC
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
CB chung
=>ΔNBC=ΔMCB
=>góc GBC=góc GCB
=>ΔGCB cân tại G
c: góc ECG+góc BCG=90 độ
góc GBC+góc GEC=90 độ
mà góc BCG=góc GBC
nên góc ECG=góc GEC
=>GC=GE=GB
=>G là trung điểm của BE
Xét ΔEBC có GD//CB
nên GD/CB=EG/EB=1/2
=>CB=2GD
