Cho hai đtròn (O;R) VÀ (O';R') TIẾP XÚC NGOÀI TẠI A. Gọi BC và DE là các tiếp tuyến chung ngoài của hai đtròn ( B và D đtròn tâm O).Chứng minh BDEC là hthang cân và tính diện tích hthang đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QH
9 tháng 8 2015
Tóm tắt thôi nhé
a) Các cạnh // => Hình bình hành
T/g OBE = t/g OCD (^B=^C=90*, OB=OC, ^BOE=^COD vì cùng phụ với EOD) => OE = OD (2 cạnh kề) => Hình thoi
b) Nối OO' => 2 tam giác cân cùng góc đáy => so le trong => //
c) 1] OO' là đường trung trực của AB => đường trung bình
2] CB//OO'
Cm tương tự 1] để được BD//OO' => Ơ-clit => thẳng hàng
6 tháng 1 2023
a: Xét (O) có
MB,MA là tiếp tuyến
nên MB=MA
Xét (O') cos
MA,MC là tiếp tuyến
nên MA=MC=>MA=BC/2
Xét ΔABC có
AM la trung tuyến
AM=BC/2
Do đó; ΔABC vuông tại A
b: Gọi H là trung điểm của OO'
Xét hình thang OBCO' có
M,H lần lượt là trung điểm của BC,OO'
nên MH là đường trung bình
=>MH//BO//CO'
=>MH vuông góc với BC
=>BC là tiếp tuyến của (H)
TM
23 tháng 5 2023
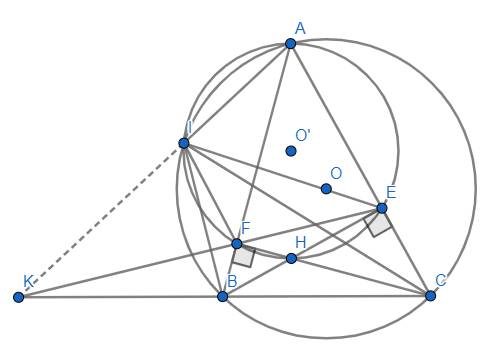
(a) Gọi \(O'\) là tâm đường tròn ngoại tiếp tứ giác \(AIFE.\)
Ta có : \(\hat{IEF}=\hat{IAF}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{IEF}=\hat{IAB}.\)
Mà : \(\hat{IAB}=\hat{ICB}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(IB\)).
Do đó, \(\hat{IEF}=\hat{ICB}.\)
Ta cũng có : \(\hat{FIE}=\hat{FAE}\) (\(AIFE\) nội tiếp đường tròn \(\left(O'\right)\)) hay \(\hat{FIE}=\hat{BAC}.\)
Mà : \(\hat{BAC}=\hat{BIC}\) (hai góc nội tiếp đường tròn \(\left(O\right)\) cùng chắn cung \(BC\)).
Do đó, \(\hat{FIE}=\hat{BIC}.\)
Xét \(\Delta IBC,\Delta IFE:\left\{{}\begin{matrix}\hat{ICB}=\hat{IEF}\left(cmt\right)\\\hat{BIC}=\hat{FIE}\left(cmt\right)\end{matrix}\right.\Rightarrow\Delta IBE\sim\Delta IFE\left(g.g\right)\) (đpcm).
(b) Mình tạm thời chưa nghĩ ra nhé:)
