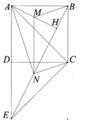
Cho hình vuông ABCD. Gọi E là điểm đối xứng với A qua D
a, CM: Tam giác ACE vuông cân
b, Kẻ AH vuông góc BE. Gọi M, N lần lượt laftrung điểm của AH và HE. CM: BMNC là hình bình hành
c, CM: M là trực tâm tam giác ANB
d, CM: Góc ANC= 90 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 11 2019
a) Xét tam giác ACE có: DC vừa là trung tuyến vừa là đường cao của tam giác ACE
\(\Rightarrow\Delta ACE\)cân tại C (1)
Vì ABCD là hình vuông (gt)
\(\Rightarrow AC\)là tia phân giác của góc BCD (tc)
\(\Rightarrow\widehat{C1}=\widehat{C2}=\frac{1}{2}.\widehat{C}=\frac{1}{2}.90^0=45^0\)
Mà ACE là tam giác cân tại C(cmt)
\(\Rightarrow DC\)là phân giác của \(\widehat{ACE}\)
\(\Rightarrow\widehat{C1}=\widehat{DCE}=\frac{1}{2}\widehat{ACE}\)Mà \(\widehat{C1}=45^0\)
\(\Rightarrow45^0=\frac{1}{2}\widehat{ACE}\)
\(\Rightarrow\widehat{ACE}=90^0\left(2\right)\)
Từ (1) và (2) \(\Rightarrow ACE\)là tam giác vuông cân.
b) Xét tam giác AHE có:
M là trung điểm của AH (gt) , N là trung điểm của HE (gt)
\(\Rightarrow MN\)là đường trung bình tam giác AHE
\(\Rightarrow MN//AE\)và \(MN=\frac{1}{2}AE\)
\(\Rightarrow MN//AD\)và \(MN=AD\)( AD=DE=1/2AE)
Mà \(AD//BC\)và \(AD=BC\)( vì ABCD là hình vuông )
\(\Rightarrow MN//BC\)và \(MN=BC\)
Xét tứ giác BMNC có:
\(\hept{\begin{cases}MN//BC\left(cmt\right)\\MN=BC\left(cmt\right)\end{cases}\Rightarrow DMNC}\)là hình bình hành
c) Ta có: \(\hept{\begin{cases}AD\perp AB\\AD//MN\end{cases}\Rightarrow}MN\perp AB\)
Xét tam giác ANB có:
\(\hept{\begin{cases}MN\perp BA\left(cmt\right)\\AH\perp NB\left(gt\right)\end{cases}}\)và MN cắt AH tại M
\(\Rightarrow M\)là trực tâm tam giác ANB
d) Vì BMNC là hình bình hành (cmt)
\(\Rightarrow BM//NC\)(3)
Vì M là trực tâm tam giác ANB(cmt)
\(\Rightarrow BM\perp AN\)(4)
Từ (3) và (4) \(\Rightarrow NC\perp AN\)
\(\Rightarrow\widehat{ANC}=90^0\)
23 tháng 11 2019
Cô ra có 1 bài mà hỏi hết luôn à, mách cô chép mạng nhá :>>>
:)))))
12 tháng 12 2021
a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông tại C
21 tháng 2 2022
a: Xét ΔACE có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔACE cân tại C
Xét ΔACE cân tại C có
CD là đường trung tuyến
CD=AE/2
Do đó: ΔACE vuông cân tại C
b: Xét ΔHEA có
M là trung điểm của HA
N là trung điểm của HE
Do đó:MN là đường trung bình
=>MN//AE và MN=AE/2
=>MN//BC và MN=BC
=>BMNC là hình bình hành
CM
16 tháng 10 2019
a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.
Þ D A C ^ = 450 Þ DACE vuông cân.
b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.
c) Do AH ^ BN, mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.
d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ A N C ^ = 900
10 tháng 12 2021
a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông cân tại C
