tim x thuoc z biet (x-5)^x+1-(x-5)^x+5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 1 2017
x + 5 chia hết cho x - 2
=> x + 5 = x - 2 + 7
ta có : x - 2 chia hết cho x - 2 nên để x + 5 chia hết cho x - 2 thì 7 phải chia hết cho x - 2
=> x - 2 \(\in\)Ư ( 7 ) = { 1 ; 7 ; -1 ; -7 }
Lập bảng ta có :
| x - 2 | 1 | 7 | -1 | -7 |
| x | 3 | 9 | 1 | 5 |
Vậy x = { 3 ; 9 ; 1 ; 5 }
NT
1
YN
27 tháng 4 2022
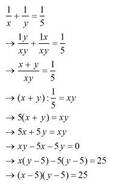
Ta xét:
\(\left(x-5\right)\left(y-5\right)=25\Leftrightarrow x-5=y-5=5\Leftrightarrow x=y=10\)
\(x-5=y-5=-5\Leftrightarrow x=y=0\)
\(\left\{{}\begin{matrix}x-5=1\\y-5=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=30\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-1\\y-5=-25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\y=-20\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=25\\y-5=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=30\\y=6\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-25\\y-5=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-20\\y=4\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(10;10\right),\left(0;0\right),\left(6;30\right),\left(4;-20\right),\left(30;6\right),\left(-20;4\right)\right\}\)
15 tháng 7 2015
a) Áp dụng t/ của dãy tỉ số = nhau, ta có:
x/5=y/3=z/4=x-z/5-4=7/1=7
Khi đó x/5=7=>x=35
y/3=7=>y=21
z/4=7=>z=28
Vậy _________
b) Mình sửa lại đề cho bạn nhé, bạn bị sai 1 chỗ: tim x,y thuộc z biết x/3=y/4=z/5 và 2x+3y+5z=86
Ta có: x/3=y/4=z/5 <=>2x/6=3y/12=5z/25
Áp dụng t/c của dãy tỉ số = nhau, ta có:
x/3=y/4=z/5=2x/6=3y/12=5z/25= (2x+3y+5z)/6+12+25= 86/43=2
Khi đó: x/3=2=>x=6
y/4=2=>y=8
z/5=2=>z= 10
Vậy _________
VN
0
WH
19 tháng 2 2018
\(\left(x-5\right)^2=0\)
\(\Rightarrow x-5=0\)
\(\Rightarrow x=0+5\)
\(\Rightarrow x=5\)
Vậy x=5
20 tháng 2 2018
(x - 5)2 = 0
=> (x - 5)2 = 02
=> x - 5 = 0
=> x = 0 + 5
=> x = 5
Vậy x = 5
BN
15 tháng 1 2017
xy - 2x - 3y = 5
<=> xy - 2x - 3y + 6 = 11
<=> x(y - 2) - 3(y - 2) = 11
<=> (x - 3)(y - 2) = 11
| x - 3 | 1 | -1 | 11 | -11 |
| y - 2 | 11 | -11 | 1 | -1 |
| x | 4 | 2 | 14 | -8 |
| y | 13 | -9 | 3 | 1 |
Vậy...
DH
1
16 tháng 9 2018
a) (x-1).(x+2) < 0
TH1: x - 1< 0
x < 1
TH2: x + 2 < 0
x < -2
b) ( x +3).(x-5) > 0
TH1: x + 3 > 0
x> -3
TH2: x - 5 > 0
x > 5
KL: x > 5
