Nếu điểm M nằm trong đường tròn tâm O bán kính 4cm. Khi đó:
A. OM < 4cm
B. OM = 4cm
C. OM > 4cm
D. OM ≥ 4cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
1
11 tháng 1 2023
a: Xét (O) có
MN,MP là tiếp tuyến
nên MN=MP
mà ON=OP
nên OM là trung trực của NP
b: Gọi giao của NP và OM là H
=>H là trung điểm của NP và NP vuông góc với OM tại H
\(NM=\sqrt{4^2-2^2}=2\sqrt{3}\left(cm\right)\)
=>\(NH=2\cdot\dfrac{2\sqrt{3}}{4}=\sqrt{3}\left(cm\right)\)
=>\(NP=2\sqrt{3}\left(cm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2022
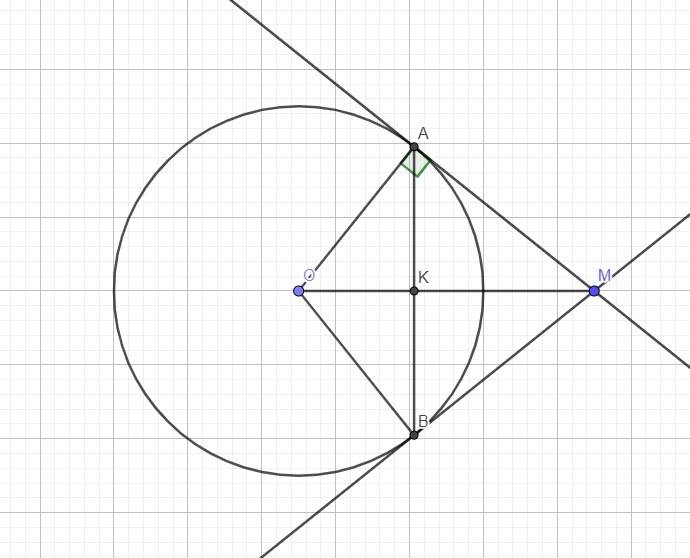
Do MA là tiếp tuyến \(\Rightarrow OA\perp MA\) hay tam giác OAM vuông tại A
Áp dụng định lý Pitago:
\(MA=\sqrt{OM^2-OA^2}=\sqrt{\left(\dfrac{8R}{5}\right)^2-R^2}=\dfrac{R\sqrt{39}}{5}\)
Theo t/c hai tiếp tuyến cắt nhau ta có \(AM=BM\)
Mà \(OA=OB=R\Rightarrow OM\) là trung trực AB \(\Leftrightarrow\left\{{}\begin{matrix}OM\perp AB\\AK=BK\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông OAM:
\(AK.OM=OA.AM\Rightarrow AK=\dfrac{OA.AM}{OM}=\dfrac{R\sqrt{39}}{8}\)
\(\Rightarrow AB=2AK=\dfrac{R\sqrt{39}}{4}\)
Áp dụng định lý Pitago trong tam giác vuông AOK:
\(OK=\sqrt{OA^2-AK^2}=\sqrt{R^2-\left(\dfrac{R\sqrt{39}}{8}\right)^2}=\dfrac{5R}{8}\)
Vì điểm M nằm trong đường tròn tâm O bán kính 4cm nên OM < 4cm.