Cho \(\Delta ABC\)vuông tại A. AB<AC thỏa mãn BC2=4AB.AC. Tính số đo các góc nhọn của \(\Delta ABC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2021
a) Áp dụng HTL ta có:\(MH.HP=MH^2\Rightarrow x=\sqrt{2.8}=4\)
\(BC=MH+HP=10\)
Áp dụng HTL ta có: \(HP.NP=MP^2\Rightarrow y=\sqrt{8.10}=4\sqrt{5}\)
b) Áp dụng HTL ta có: \(EQ.QF=DQ^2\Rightarrow x=\dfrac{4^2}{1}=16\)
\(EF=EQ+QF=17\)
Áp dụng HTL ta có: \(QP.EF=y^2\Rightarrow y=\sqrt{17.1}=\sqrt{17}\)
21 tháng 3 2023
a: Xet ΔABD vuông tại B và ΔAHD vuông tại H có
AD chung
góc BAD=góc HAD
=>ΔABD=ΔAHD
b; AB=AH
DB=DH
=>AD là trung trực của BH
c: Xet ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
góc BDI=góc HDC
=>ΔBDI=ΔHDC
=>DI=DC
=>ΔDIC cân tại D
d: Xét ΔAIC có AB/BI=AH/HC
nên BH//IC
e: AD vuông góc BH
BH//IC
=>AD vuông góc IC
10 tháng 5 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
2
8 tháng 5 2023
`a)` Xét `\triangle ABC` vuông tại `A` có: `\hat{B}+\hat{C}=90^o`
Xét `\triangle ABH` vuông tại `H` có: `\hat{B}+\hat{A_1}=90^o`
`=>\hat{C}=\hat{A_1}`
Xét `\triangle ABC` và `\triangle HBA` có:
`{:(\hat{C}=\hat{A_1}),(\hat{B}\text{ là góc chung}):}}=>\triangle ABC` $\backsim$ `\triangle HBA` (g-g)
`b)` Ta có: `BC=HB+HC=4+9=13(cm)`
Xét `\triangle ABC` vuông tại `A` có: `AH` là đường cao
`@AH=\sqrt{BH.HC}=6 (cm)`
`@AB=\sqrt{BH.BC}=2\sqrt{13}(cm)`
Ta có: `\hat{DEA}=\hat{ADH}=\hat{AEH}=90^o`
`=>` Tứ giác `AEHD` là hcn `=>DE=AH=6(cm)`
`c)` Xét `\triangle AHB` vuông tại `H` có: `HD \bot AB=>AH^2=AD.AB`
Xét `\triangle AHC` vuông tại `H` có: `HE \bot AC=>AH^2=AE.AC`
`=>AD.AB=AE.AC`
29 tháng 4 2023
a: Xet ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=90 độ và AD=DE
AD=DE
DE<DC
=>AD<DC
16 tháng 4 2021
a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)
16 tháng 4 2021
a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)
d) ΔEAD ∼ ΔBAC
ΔABC vuông tại A, theo định lí Pytago:
Theo b, ta có:
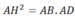
Theo định lý Pi-ta-go, ta có \(BC^2=AB^2+AC^2\)
Vậy nên theo bài ra ta có \(AB^2+AC^2=4AB.AC\)
\(\Rightarrow AB^2-4AB.AC+AC^2=0\)
\(\Rightarrow\left(\frac{AB}{AC}\right)^2-4.\frac{AB}{AC}+1=0\)
Đặt \(\frac{AB}{AC}=k\Rightarrow k^2-4k+1=0\Rightarrow\orbr{\begin{cases}k=2+\sqrt{3}\\k=2-\sqrt{3}\end{cases}}\)
Do AB < AC nên \(\frac{AB}{AC}< 1\), vậy ta lấy \(k=2-\sqrt{3}\)
Với \(k=2-\sqrt{3}\Rightarrow tan\widehat{ACB}=2-\sqrt{3}\Rightarrow\widehat{ACB}=15^o\Rightarrow\widehat{ABC}=75^o\)
Cô Huyền giúp em rõ hơn được không, em lớp 8 chưa học \("\tan"\)