Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. Gọi M là một điểm bất kì thuộc cung BC.
a) Chứng minh rằng MA = MB + MC
b) Gọi D là giao điểm của MA và BC. Chứng minh rằng \(\frac{MD}{MB}+\frac{MD}{MC}=1\)
c) Tính tổng MA^2 + MB^2 MC ^2 theo R.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1 2018
a, Trên AM lấy điểm E sao cho ME = MB
Có : góc BME = góc BCA = 60 độ
=> tam giác EMB đều => EB = MB và góc EMB = 60 độ
Góc EMB = 60 độ => góc EBC + góc CBM = 60 độ
Lại có : góc ABC = 60 độ nên góc ABE + góc EBC = 60 độ
=> góc ABE = góc CBM
=> tam giác AEB = tam giác CMB (c.g.c)
=> AE = CM
=> AM = AE + EM = CM+BM
14 tháng 1 2018
b, Theo câu a có tam giác AEB = tam giác CMB
=> góc EAB = góc MCB
=> tam giác MDC đồng dạng tam giác MBA (g.g)
=> MC/MA = MD/MB
=> MD.MA=MB.MC
Có : MD/MB + MD/MC = MD.(1/MB + 1/MC) = MD.(MB+MC)/MB.MC = MD/MA/MB.MC = 1
CM
5 tháng 3 2017
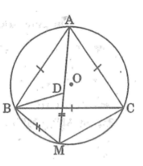
Ta có: ∆ ABD = ∆ CBM (cmt)
suy ra: AD = CM
Ta có: DM = BM ( tam giác MBD đều )
mà AM = AD + DM
suy ra: MA = MC + MB
19 tháng 4 2017
Lười quá, chắc mình giải câu c thôi ha.
Vẽ \(OH\) vuông góc \(d\) tại \(H\). \(AB\) cắt \(OH\) tại \(L\). \(OM\) cắt \(AB\) tại \(T\)
.
CM được \(OL.OH=OT.OM=R^2\) nên \(L\) cố định. Vậy \(AB\) luôn qua \(L\) cố định.
HD
11 tháng 2 2019
a ) Ta có BM=MD (gt)
=> \(\Delta\)MBD cân tại M
Mặt khác \(\widehat{AMB}=\widehat{ACB}\) ( Hai góc nội tiếp chắn cung AB)
Mà \(\widehat{ACB}=60^0\)( tam giác ABC đều)
Suy ra \(\widehat{AMB}=60^0hay\widehat{DMB}=60^0\)
Vậy \(\Delta MBD\) đều
b) Ta có \(\Delta MBD\) đều ( CMT)
Suy ra : \(\widehat{DMB}=\widehat{DBC}+\widehat{CBM}=60^0\)(1)
Lại có : tam giác ABC đều (gt)
Suy ra : \(\widehat{ABC}=\widehat{ABD}+\widehat{DBC}=60^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ABD}=\widehat{MBC}\)
Xét hai tam giác ABD và CBM ta có
BC=BA (gt)
\(\widehat{ABD}=\widehat{MBC}\left(cmt\right)\)
BD=BM( tam giác MBD đều)
=> \(\Delta ABD=\Delta CBM\left(c.g.c\right)\)
c)\(\Delta ABD=\Delta CBM\left(cmt\right)\)
SUy ra AD=CM
mà AM=AD+DM
SUy ra MA=MC+MD
