Cho tam giác ABC có góc A=90o.E là một điểm nằm trong tam giác ABC. Chứng minh rằng góc BEC là góc tù
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
28 tháng 7 2015
Ta có tam giác ABC = 90 độ nên
góc ABC +góc ACB = 90 độ
vì lấy điểm E nằm trong tam giác nên
góc ABE + EBC + ACE + ECB = 90 độ
=> góc EBC + ECB < 90 độ
nên góc BEC > 90 độ
3 tháng 11 2016
Ta có hình vẽ:
Ta có: ABC + ACB = 90o
Dễ thấy: EBC < ABC; BCE < ACB
=> EBC + BCE < ABC + ACB = 90o
Xét Δ BEC có: EBC + BCE + BEC = 180o (tổng 3 góc của Δ)
Do EBC + BCE < 90o nên BEC > 90o
Mà BEC < 180o => BEC là góc tù (đpcm)
PT
1
CM
7 tháng 1 2018
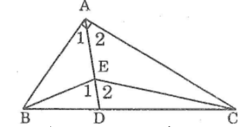
Kéo dài AE cắt BC tại D
Trong ∆ABE ta có ∠E1 là góc ngoài tại đỉnh E
Suy ra: ∠E1 > ∠A1 (tính chất góc ngoài tam giác)(1)
Trong ∆AEC ta có ∠E2 là góc ngoài tại đỉnh E
Suy ra: ∠E2 > ∠A2 (tính chất góc ngoài tam giác)(2)
Cộng từng vế (1) và (2) ta có:
∠E1 + ∠E2 > ∠A1 +∠A2
Hay ∠ (BEC) > ∠ (BAC) = 90º
Vậy góc (BEC) là góc tù.
TT
0
TT
0
VQ
18 tháng 1 2016
ta có ABC+ACB=90(TC \(\Delta\) vuông)
E\(\in\Delta\) đó \(\Rightarrow\) EBC+ECB<90\(\Rightarrow\) BEC>90 \(\Rightarrow\) BEC tù
TT
0
2 tháng 3 2022
Bài 2:
Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB
Ta có tam giác ABC = 90 độ nên
\(\widehat{ABC}+\widehat{ACE}=90^0\)
Vì lấy điểm E nằm trong tam giác nên\(\widehat{ABE}+\widehat{EBC}+\widehat{ACE}+\widehat{ECB}=90^0\)
\(\Rightarrow\)\(\widehat{EBC}+\widehat{ECB}< 90^0\); \(\widehat{EBC}+\widehat{ECB}< 90^0\)
Nên \(\widehat{BEC}>90^0\)