Cho hình vuông ABCD. M là một điểm tùy ý trên đường chéo BD. KẺ ME vuông góc AB, MF vuông góc AD
a) Chứng minh DE=CF Và DE vuông góc CF
B) CMR ba đường thẳng DE, BF, CM đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
23 tháng 6 2021
Xét \(\Delta DFM\) vuông tại F có \(\angle FDM=45\Rightarrow\Delta DFM\) vuông cân tại F
\(\Rightarrow DF=FM\)
Vì \(\angle MFA=\angle MEA=\angle EAF=90\Rightarrow AEMF\) là hình chữ nhật
\(\Rightarrow AE=FM=DF\)
Xét \(\Delta DCF\) và \(\Delta ADE:\) Ta có: \(\left\{{}\begin{matrix}AD=CD\\DF=AE\\\angle DAE=\angle CDF=90\end{matrix}\right.\)
\(\Rightarrow\Delta DCF=\Delta ADE\left(c-g-c\right)\Rightarrow DE=CF\)
b) \(\Delta DCF=\Delta ADE\Rightarrow\angle DCF=\angle ADE\)
\(\Rightarrow\angle DCF+\angle DFC=\angle ADE+\angle DFC\Rightarrow\angle ADE+\angle DFC=90\)
\(\Rightarrow DE\bot FC\)
Tương tự chứng minh được: \(BF\bot CE\)
Gọi giao điểm của DE,BF là H \(\Rightarrow H\) là trực tâm tam giác CEF
\(\Rightarrow CH\bot EF\left(1\right)\)
FM cắt CB tại G,CM cắt AD tại I
Dễ dàng chứng minh được DCFG là hình chữ nhật
\(\Rightarrow CG=DF=AE\)
Ta có: \(MG=FG-FM=CD-FD==AD-FD=AF\)
Xét \(\Delta CMG\) và \(\Delta EFA:\) Ta có: \(\left\{{}\begin{matrix}MG=AF\\AE=CG\\\angle CGM=\angle EAF=90\end{matrix}\right.\)
\(\Rightarrow\Delta CMG=\Delta EFA\left(c-g-c\right)\Rightarrow\angle AFE=\angle CMG=\angle FMI\)
\(\Rightarrow\angle AFE+\angle FIM=\angle FMI+\angle FIM\Rightarrow\angle AFE+\angle FIM=90\)
\(\Rightarrow CM\bot EF\left(2\right)\)
Từ (1) và (2) \(\Rightarrow C,H,M\) thẳng hàng \(\Rightarrow\) đpcm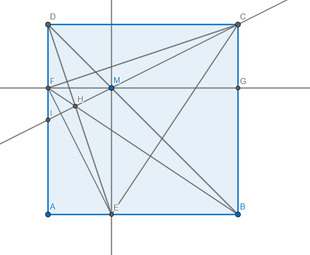
16 tháng 2 2018
à nhầm ngay cái chỗ từ 1 ở câu a và 2
bạn sửa lại dùm mình thành từ 1 và 2 nha mình viết nhầm
16 tháng 2 2018
Dễ thấy AEMF là hình chữ nhật => AE = FM
Dễ thấy tg DFM vuông cân tại F => FM = DF
=> AE = DF => tg vuông ADE = tg vuông DCF ( AE = DF; AD = DC) => DE = CF
tg vuông ADE = tg vuông DCF => ^ADE = ^DCF => DE vuông góc CF (1) ( vì đã có AD vuông góc DC)
Tương tự dễ thấy AF = BE => tg vuông ABF = tg vuông BCE => ^ABF = ^BCE => BF vuông góc CE ( vì đã có AB vuông góc BC) (2)
Gọi H là giao điểm của BF và DE
Từ (1) ở câu a) và (2) => H là trực tâm của tg CEF
Mặt khác gọi N là giao điểm của BC và MF. dễ thấy CN = DF = AE: MN = EM = A F => tg vuông AEF = tg vuông CMN => ^AEF = ^MCN => CM vuông góc EF ( vì đã có CN vuông góc AE) => CM là đường cao thuộc đỉnh C của tg CE F => CM phải đi qua trực tâm H => 3 đường thẳng DE;BF,CM đồng quy tại H
17 tháng 3 2016
a) xet tg DEA va tg DFC ta co;
A=D=90 ; AD=DC; AE=MF=DF ( vi tg DFM vuong can)
vay 2 tg = nhau => DE=CF
b) h di em lam
c)diem M se nam o giao diem 2 dg cheo khi do AEMF la hinh vuong se co Smax
( em hoc lop 6 ma chang nat oc j )
22 tháng 5 2021
a, \(AEMF\)là hình chữ nhật nên \(AE=FM\)
\(DFM\)vuông cân tại \(F\)suy ra \(FM=DF\)
\(\Rightarrow AE=DF\)suy ra \(\Delta ADE=\Delta DCF\)
\(\Rightarrow DE=CF\)
b, Tương tự câu a, dễ thấy \(AF=BE\)
\(\Rightarrow\Delta ABF=\Delta BCE\)
\(\Rightarrow\widehat{ABF}=\widehat{BCE}\) nên \(BF\)vuông góc \(CE\)
Gọi \(H\)là giao điểm của \(BF\)và \(DE\)
\(\Rightarrow H\)là trực tâm của tam giác \(CEF\)
Gọi \(N\)là giao điểm của \(BC\)và \(MF\)
\(CN=DF=AE\)và \(MN=EM=AF\)
\(\Delta AEF=\Delta CMN\)
\(\Rightarrow\widehat{AEF}=\widehat{MCN}\)
\(\Rightarrow CM\perp EF\)
\(\Rightarrow\)Ba đường thẳng DE,BF,CM đồng quy tại H
c, \(AE+EM=AE+EB=AB\)không đổi
\(\left(AE-EM\right)^2\ge0\Rightarrow AE^2+AM^2\ge2AE.AM\)
\(\Rightarrow\left(AE+AM\right)^2\ge4AE.AM\Rightarrow\left(\frac{AE+EM}{2}\right)^2=\frac{AB^2}{4}\ge AE.AM=S_{AEMF}\)
Vậy \(S_{AEMF}max\)khi \(AE=EM\)( M là giao AC và và BD )
CH
Cô Hoàng Huyền
Admin
VIP
24 tháng 2 2018
Câu hỏi của Kunzy Nguyễn - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
CH
Cô Hoàng Huyền
Admin
VIP
24 tháng 2 2018
Câu hỏi của Kunzy Nguyễn - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
20 tháng 7 2020
cô Quản Lý Hoàng Thị Thu Huyền ơi cô bảo tham khảo ở đâu thế ạ ? sao em ko thấy đường link hay bài đăng j vậy
Câu hỏi của Kunzy Nguyễn - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.