Hình thoi ABCD có đường chéo AC và BD cắt nhau tại điểm O, OA bằng 3 cm, OB bằng 4 cm, AB bằng 5 cm. Tính diện tích, chu vi của hình thoi ABCD.
Nhớ giải chi tiết giúp mk nha ! Cảm ơn các bạn !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 11 2019
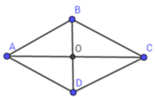
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
CM
9 tháng 5 2017
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B
CM
23 tháng 11 2019
Độ dài đường chéo BD là:
40×35=24(cm)
Diện tích hình thoi ABCD là:
40×24:2=480( c m 2 )
Vì hình chữ nhật GHIK có diện tích bằng diện tích hình thoi ABCD nên diện tích hình chữ nhật GHIK là 480 c m 2 .
Chiều dài hình chữ nhật là:
480:15=32(cm)
Chu vi hình chữ nhật là:
(32+15)×2=94(cm)
Đáp số: 94cm.
Vậy đáp án đúng điền vào ô trống là 94.
B. Diện tích hình thoi lớn hơn diện tích hình vuông đúng/sai 
C. Diện tích hình thoi bé hơn diện tích hình vuông đúng/ sai
VN
9 tháng 5 2022
Độ dài đường chéo BD là :
\(20\times\dfrac{3}{5}=12\left(cm\right)\)
Diện tích hình thoi ABCD là :
\(\dfrac{20\times12}{2}=120\left(cm^2\right)\)
Đ/S : \(120cm^2\)
26 tháng 8 2016
Vì \(\frac{AC}{BD}=1,05\)
\(\Rightarrow\frac{\frac{1}{2}AC}{\frac{1}{2}BD}=1,05\)
\(\Rightarrow\frac{AO}{BO}=1,05\)
\(\Rightarrow AO=1,05.BO\)
Xét \(\Delta AOB\)vuông tại O ( vì O là giao điểm 2 đường chéo hình thoi ) có :
\(AO^2+BO^2=AB^2\)( Định lý Pytago )
\(\left(1,05.BO\right)^2+BO^2=58^2\)
\(2,1025BO^2=3364\)
\(\Rightarrow BO^2=1600\)
\(\Rightarrow BO=40\) \(\left(BO>0\right)\)
\(\Rightarrow AC=\left(BO.1,05\right).2=84\)(cm)
Vậy ...
