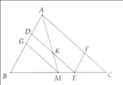
cho tam giác ABC có AM là đường trung tuyến D là điểm nằm giữa B M Qua D kẻ đường thẳng song song với AM đường thẳng d cắt 2 đường thẳng AB AC thứ tự tại E F kẻ aK song song với BC
a CM 2 tam giác KAE và MBA đồng dạng với nhau
b cm K là trung điểm của EF
c gọi AN là trung điểm của AK O là giao điểm của DN và AB xấc định vị trí của điểm D trên đoạn thẳng BM để OD:ND=2:5