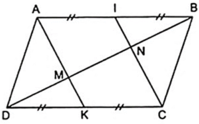
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB và CD, M và N là giao điểm của AI và CK với BD
a) Chứng minh : AI song song với CK
b) Chứng minh DM=MN=NB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
25 tháng 10 2021
a) Ta có: AK = 1212 AB
IC = 1212 DC
mà AB = DC (vì ABCD là hình bình hành)
=> AK = IC
=> AK // IC (vì AB // DC)
=> AKCI là hình bình hành
=> AI // KC
b) Xét ΔABMΔABM có:
AK = KB (gt)
AM // KN (vì AI // KC)
=> BN = MN (1)
Xét ΔDNCΔDNC có:
DI = IC (gt)
IM // CN (vì AI // KC)
=> DM = MN (2)
Từ 1 và 2 =>DM=MN=NB
CM
19 tháng 12 2017
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: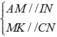
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
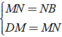⇒ DM = MN = NB
CM
5 tháng 3 2019
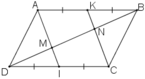
a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.
AH
Akai Haruma
Giáo viên
7 tháng 10 2021
Lời giải:
a. $I\in AD, K\in CB$ mà $AD\parallel CB$ (tính chất hình bình hành)
$\Rightarrow AI\parallel CK$
b.
Do $E$ là trung điểm $AB$ nên $AE=\frac{1}{2}AB$
Do $F$ là trung điểm $CD$ nên $CF=\frac{1}{2}CD$
Mà $AB=CD$ (tính chất hbh)
$\Rightarrow AE=CF$
c.
Tính chất hbh phát biểu rằng 2 đường chéo cắt nhau tại trugn điểm mỗi đường
Do đó $AC$ cắt $BD$ tại trung điểm $BD$. Mà trung điểm của $BD$ là $O$ nên $A,O,C$ thẳng hàng
a ) AK = 1/2 AB
CI = 1/2 CD
Mà AB //= CD nên AK //= CI suy ra
AKCI - hình bình hành
Nên AI // CK
b ) Xét t/g DNC có :
I là trung điểm CD mà IM // NC
=> IM là đường trung bình của t/g DNC
=> MD = MN ( 1 )
Xét t/g ABM có :
K là trung điểm AB mà KN // AM
=> KN là đường trung bình của t/g ABM ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra DM = MN = NB