Một người đi xe đạp nửa qđg đầu với vận tốc v1=45km/h, đi nửa quãng đường còn lại với vận tốc v2 ko đổi. Bt các Đoạn đường mà ng ấy đi là thẳng và vận tốc trung bình trên cả quãng đường là 36km/h. Tính vận tốc v2?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}\Rightarrow10=\dfrac{S_{tổng}}{\dfrac{S_{tổng}}{15}+\dfrac{S_{tổng}}{v_2}}=\dfrac{S_{tổng}}{S_{tổng}\left(\dfrac{1}{15}+\dfrac{1}{v_2}\right)}=\dfrac{1}{\dfrac{1}{15}+\dfrac{1}{v_2}}\)
\(\Rightarrow\dfrac{1}{v_2}=\dfrac{1}{10}-\dfrac{1}{15}=\dfrac{1}{30}\Rightarrow v_2=30\left(\dfrac{km}{h}\right)\)

\(=>vtb=\dfrac{S}{\dfrac{\dfrac{1}{2}S}{v1}+\dfrac{\dfrac{1}{2}S}{v2}}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{2v2}}=\dfrac{S}{\dfrac{S\left(2v2+40\right)}{80v2}}=\dfrac{80v2}{2v2+40}=15\)
\(=>v2=12km/h\)

Gọi S là chiều dài quãng đường ta có :
Thời gian đi hết nửa quãng đường đầu là :\(t_1=\frac{S}{2v_1}\)
Thời gian đ hết nửa quãng đường sau là :
\(t_2=\frac{S}{2v_2}\)
Vận tốc trung bình trên cả quãng đường S là :
\(v_{tb}=\frac{S}{\left(t_1+t_2\right)}\Rightarrow\left(t_1+t_2\right)=\frac{S}{v_{tb}}\)
Từ các điều nói trên : \(\frac{1}{v_1}+\frac{1}{v_2}=\frac{2}{v_{tb}}\)
Thế số vào tính được v2 = 7,5 km/h
ta có:
thời gian người đó đi trong nửa quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{30}\)
thời gian người đó đi trong quãng đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{30}+\frac{S}{2v_2}}=\frac{S}{S\left(\frac{1}{30}+\frac{1}{2v_2}\right)}=\frac{1}{\frac{1}{30}+\frac{1}{2v_2}}\)
\(\Leftrightarrow10=\frac{1}{\frac{v_2+15}{30v_2}}=\frac{30v_2}{v_2+15}\)
giải phương trình trên ta có:
v2=7,5km/h

Ta có: \(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}\)
\(\Leftrightarrow9=\dfrac{\dfrac{2}{3}s+\dfrac{1}{3}s}{\dfrac{\dfrac{2}{3}s}{12}+\dfrac{\dfrac{1}{3}s}{v_2}}=\dfrac{s}{\dfrac{s}{18}+\dfrac{s}{3v_2}}=\dfrac{s}{\dfrac{s\left(18+3v_2\right)}{54v_2}}=\dfrac{54v_2}{18+3v_2}\)
\(\Leftrightarrow v_2=6\left(\dfrac{m}{s}\right)\)

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
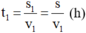
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
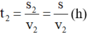
Vậy tổng thời gian đi hết cả quãng đường là: 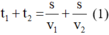
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
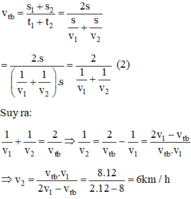

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:

Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:

Vậy tổng thời gian đi hết cả quãng đường là: 
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:

Giải
Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=s/v1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=s/v2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb = 2s/t1+ t2 (3)
Kết hợp (1); (2); (3) có: 1/v1 + 1/v2 = 2/vtb
Thay số vtb = 8km/h ; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h.
Gọi nửa quãng đường là \(x\) thì cả quãng đường là \(2x\).
Thời gian người đó đ nửa quãng đường đầu là: \(\frac{x}{45}\), đi nửa quãng đường sau là \(\frac{x}{v_2}\) .
Thời gian người đó đi cả quãng đường là: \(\frac{2x}{36}\).
Vậy ta có: \(\frac{x}{45}+\frac{x}{v_2}=\frac{2x}{36}\)
\(\Rightarrow\frac{1}{45}+\frac{1}{v_2}=\frac{1}{18}\)
\(\Rightarrow\frac{1}{v_2}=\frac{1}{18}-\frac{1}{45}=\frac{1}{30}\)
\(\Rightarrow v_2=30\)
Vận tốc trung bình trên cả đoạn đường :
vtb=S / S2.v1+S2.v2=2.v1.v2 / v1+v2.(km/h)
Mà vtb = 8, v1 = 12 nên v2 = 6 km/h.