Cho hình trụ ABCD nội tiếp khối cầu tâm O bán kính R, biết AB=R. Thể tích của khối cầu nằm ngoài khối trụ là:
A. \(\frac{\pi R^3}{6}\left(4-3\sqrt{3}\right)\) B.\(\frac{\pi R^3}{12}\left(16-3\sqrt{3}\right)\) C. \(\frac{\pi R^3}{12}\left(8-3\sqrt{3}\right)\) D.\(\frac{\pi R^3}{3}\left(8-3\sqrt{3}\right)\)
( Có lời giải )

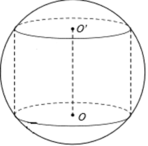
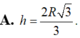
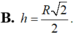
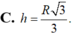
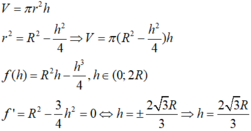
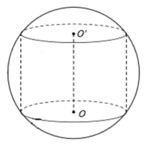
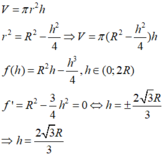
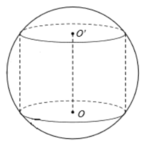
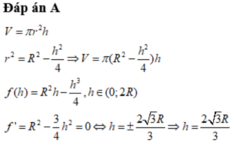

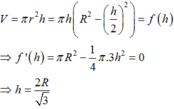
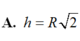
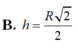
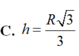
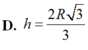
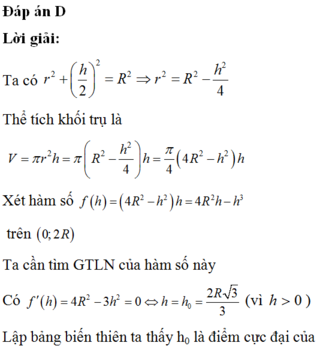
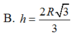
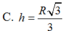
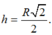
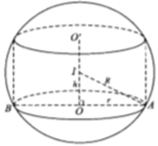

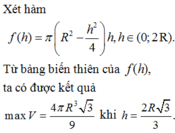
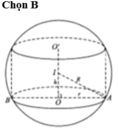

V(tru) =π.R^2/4.R√3
V(cau)=4/3.π.R^3
Vnktru=πR^3(4/3-√3/4)
=πR^3/12.(16-3√3)
Chọn (B).
Vtru =π.R^2/4.R√3
Vcau=4/3.π.R^3
Vnktru=πR^3(4/3-√3/4)
=πR^3/12.(16-3√3)
Chọn (B).