Tất cả các bài này giải theo cách của lớp 9Bài 1: (Công thức tính độ dài đường trung tuyến) Cho tam giác ABC , gọi ma là đường trung tuyến xuất phát từ đỉnh A. Chứng minh \(m^2_a=\frac{2\left(b^2+c^2\right)-a^2}{4}\)Bài 2: Cho tam giác ABC có a2+b2=2c2, ma, mb, mc là các đường trung tuyến xuất phát từ ba đỉnh A, B, C.Chứng...
Đọc tiếp
Tất cả các bài này giải theo cách của lớp 9
Bài 1: (Công thức tính độ dài đường trung tuyến)
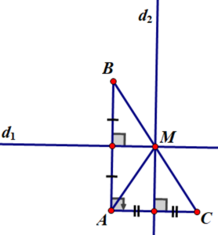
Cho tam giác ABC , gọi ma là đường trung tuyến xuất phát từ đỉnh A. Chứng minh \(m^2_a=\frac{2\left(b^2+c^2\right)-a^2}{4}\)
Bài 2: Cho tam giác ABC có a2+b2=2c2, ma, mb, mc là các đường trung tuyến xuất phát từ ba đỉnh A, B, C.Chứng minh
\(m_a+m_b+m_c=\frac{\sqrt{3}}{2}\left(a+b+c\right)\)
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha