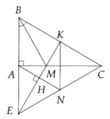
Cho tam giác ABC cân tại A. Phân giác AH. Đường trunng trực của AB cắt AH tại O. Trên các cạnh AB và AC của tam giác lấy các điểm E và F sao cho AE+AF=AB. Chứng minh OE=OF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2022
Bài 3:
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
Do đó; ΔAHB=ΔAKC
Suy ra: AH=AK và BH=CK
c: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
MB=CN
góc M=góc N
Do đó ΔHBM=ΔKCN
Suy ra: góc HBM=góc KCN
=>góc OBC=góc OCB
hay ΔOBC can tại O
I
22 tháng 2 2020
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
15 tháng 7 2018
Trong \(\Delta ABC\)cân tại A , ta có :
AH là đường p/g của góc A
\(\Rightarrow\)AH là đường trung trực của BC
OI là đường trung trực của AB
\(\Rightarrow\)O là giao điểm của 3 đường trung trực của \(\Delta ABC\)
=> OC=OA=OB
Xét \(\Delta AOC\)có:
OA=OC ( cmt )
\(\Rightarrow OAC=OCA\)
MÀ \(IAO=OAC\Rightarrow IAO=FCO\)
Xét \(\Delta OEA\)và \(\Delta OFC\)có :
AE= CF ( gt )
EAO=FOC ( cmt )
OA=OC ( cmt )
\(\Rightarrow\Delta OEA=\Delta OFFC\left(c-g-c\right)\)
\(\Rightarrow OE=OF\left(dpcm\right)\)
b, Vì OE=OF ( câu a )
\(\Rightarrow\)O thuộc đường trung trực của EF
14 tháng 5 2023
Vì các đường trung trực của `\Delta ABC` cắt nhau tại điểm O
`->` `\text {AO}` là đường trung trực thứ `3` của `\Delta`
Xét các đáp án trên `-> D.`
k nhé
hok tốt
cảm ơn nhé