Cho tam giác ABC vuông tại A, đường cao AH. Gọi E,F là hình chiếu của H lên AB,AC. Chứng minh rằng:
\(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}=\sqrt[3]{BC^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
Hệ thức lượng: \(AH^2=BH.CH\)
Hai tam giác vuông BEH và HFC đồng dạng: \(\Rightarrow\dfrac{BE}{FH}=\dfrac{EH}{CF}\Rightarrow BE.CF=EH.FH\)
Hai tam giác vuông AEH và CFH đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{EH}{FH}\Rightarrow AH.FH-CH.EH=0\)
Hai tam giác vuông BEH và AFH đồng dạng \(\Rightarrow\dfrac{BH}{AH}=\dfrac{EH}{FH}\Rightarrow EH.AH-BH.FH=0\)
Ta có: \(\left(BE\sqrt{CH}+CF\sqrt{BH}\right)^2=BE^2.CH+CF^2.BH+2BE.CF.\sqrt{BH.CH}\)
\(=BE^2.CH+CF^2.BH+2BE.CF.AH\)
\(=\left(BH^2-EH^2\right)CH+\left(CH^2-FH^2\right)BH+2BE.CF.AH\)
\(=BH.CH\left(BH+CH\right)-EH^2.CH-FH^2.BH+2EH.FH.AH\)
\(=AH^2.BC+EH\left(AH.FH-EH.CH\right)+FH\left(AH.EH-FH.BH\right)\)
\(=AH^2.BC=\left(AH\sqrt{BC}\right)^2\)
\(\Rightarrow BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)
10 tháng 8 2021
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(BE\cdot BA=BH^2\)
hay \(BE=\dfrac{BH^2}{BA}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:
\(CF\cdot CA=CH^2\)
hay \(CF=\dfrac{CH^2}{CA}\)
Ta có: \(\dfrac{BE}{CF}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{CA}\)
\(=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}\)
\(=\dfrac{AB^4\cdot AC}{AC^4\cdot AC}=\dfrac{AB^3}{AC^3}\)
31 tháng 8 2022
1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AEF=góc AHF=góc C(1)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc MCA(2)
Từ (1) và (2) suy ra góc AEF=góc C
2: Tham khảo:
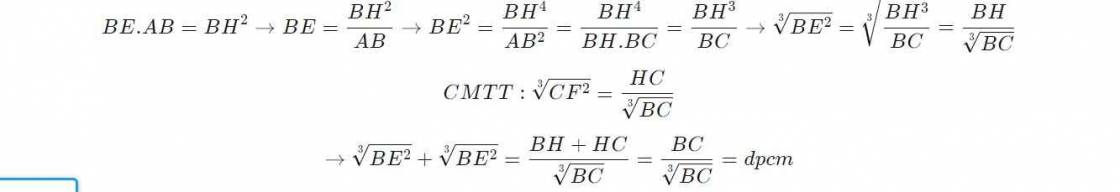
ta can cm\(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}\) =\(\sqrt[3]{BC}\)
hay \(\sqrt[3]{\frac{BE^2}{BC^2}}+\sqrt[3]{\frac{CF^2}{BC^2}}=1\)
trong tam giác AHB \(BH^2=BE.BA\Rightarrow BE=\frac{BH^2}{BA}\Rightarrow BE^2=\frac{BH^4}{BA^2}\) (1)
ma trong tam giac ABC \(AB^2=BH.BC\)
thay vao (1) ta co \(BE^2=\frac{BH^4}{AB^2}=\frac{BH^4}{BH.BC}=\frac{BH^3}{BC}\Rightarrow\frac{BE^2}{BC^2}=\frac{BH^3}{BC^3}\)
\(\Rightarrow\sqrt[3]{\frac{BE^2}{BC^2}}=\frac{BH}{BC}\)
CM TUONG TU \(\sqrt[3]{\frac{CF^2}{BC^2}}=\frac{CH}{BC}\)
VAY \(\sqrt[3]{\frac{BE^2}{BC^2}}+\sqrt[3]{\frac{CF^2}{BC^2}}=\frac{HB}{BC}+\frac{CH}{BC}=1\)