Trên đường tròn (O;2cm) cho 4 điểm A ; B ; C ; D . Lấy điểm K nằm ngoài đường tròn (O) .Gọi A' ; B' ; C' ; D' lần lượt là trung điểm của KA ; KB ; KC ; KD .Chứng minh rằng bốn điểm A' ; B' ; C' ; D' cùng nằm trên một đường tròn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 5 2022
a: \(\widehat{AMO}=90^0\)
nên điểm M chuyển động trên đường tròn đường kính AO
b: Đường tròn (O') tiếp xúc trong với đường tròn (O)
CM
3 tháng 6 2018
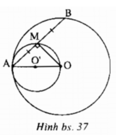
∠ (AMO) = 90 ° . Điểm M chuyển động trên đường tròn (O’) đường kính AO.
LA
3 tháng 1 2017
Mình nói sơ qua nhá:
a) Ta có ΔABO là Δ vuông tại B
Ta tính được AB=8 nhờ vào định lí Py-ta-go
b) Do I là trung điểm của CD nên OI⊥CD, lại suy ra được OI⊥IA
Nên I sẽ chuyển động trên đường tròn đường kính OA (cố định) khi C thay đổi trên đường tròn
c) Chứng minh cho ΔABD∼ΔACB
Suy ra được AC.AD=AB2 không đổi
tk nha bạn
thank you bạn
(^_^)
hình như sai đề mk ko hiểu đề này thì mk hiểu
Từ điểm A nằm ngoài đường tròn (O;R) kẻ 2 tiếp tuyến AB và AC. Gọi H là giao điểm của OA và BC. a) Chứng minh tứ giác ABOC nội tiếp. b) Tính tích OH.OA theo R
bài làm
Từ điểm A nằm ngoài đường tròn (O;R) kẻ 2 tiếp tuyến AB và AC. Gọi H là giao điểm của OA và BC.
a) Chứng minh tứ giác ABOC nội tiếp
b) Tính tích OH.OA theo R
c) Gọi E là hình chiếu của C trên đường kính BD của đường tròn tâm O. Chứng minh góc HEB bằng với góc HAB
d) AD cắt CE ở K. Chứng minh K là trung điểm của CE
e) Tính theo R diện tích hình giới hạn bởi 2 tiếp tuyến AB, AC và cung nhỏ BC của đường tròn tâm O trong trường hợp OA = 2R