Câu 1: Nếu tăng áp lực của vật lên mặt phẳng thì hệ số ma sát thay đổi như thế nào? Câu 2: Một vật trượt đều trên mặt phẳng ngang. Hệ số ma sát trượt 0,25. Tính lực ma sát giữa vật và mặt phẳng và lực kéo. Biết khối lượng của vật là 5kg, g = 10m/s2. Câu 3: Một ô tô khối lượng 1 tấn đang chuyển động với vận tốc 36km/h thì hãm phanh chuyển động chậm dần đều đến khi dừng lại. Biết hệ số ma sát trượt giữa ô tô và mặt đường là 0,2; tìm quãng đường vật chuyển động được từ khi hãm phanh đến khi dừng lại. Câu 4: Lực nào đóng vai trò là lực phát động trong các chuyển động của ô tô, xe máy ...? Câu 5: Khi đi trên đường, đôi khi ta thấy có vệt bánh xe trượt trên đường. Hãy giải thích sự hình thành của các vệt bánh xe đó và nêu tác dụng của nó ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Ta có: \(v=v_0+at\Leftrightarrow10=0+a5\Leftrightarrow a=2\) (m/s2)
b. Áp dụng định luật II-Niuton có:
\(\overrightarrow{F_{ms}}+\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}=m\overrightarrow{a}\)
Chiếu các vector lực lần lượt theo phương Ox, Oy có:
Oy: N=P
Ox: \(-N\mu_t+F=ma\) \(\Leftrightarrow-mg\mu_t+F=ma\Leftrightarrow-2.10.\mu_t+8=2.2\Rightarrow\mu_t=0,2\)
c. (Vẽ lại trục Oxy, sao cho Oy trùng với phương của \(\overrightarrow{N}\), Ox trùng với phương chuyển động)
Áp dụng định luật II-Niuton có:
\(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m\overrightarrow{a}\)
Lần lượt chiếu các vector lực lên phương Ox, Oy có:
Oy: \(N=P.cos30\)
Ox: \(-F_{ms}-P.sin30=ma\)
\(\Leftrightarrow-N\mu_{t'}-mg.sin30=ma\Leftrightarrow-mg.cos30.\mu_{t'}-mg.sin30=ma\)
\(\Leftrightarrow-10.cos30.0,3-10.sin30=a\Leftrightarrow a=-7,6\) (m/s2)

a) Theo định luật công cơ học, ta phải thực hiện một công là:A=F.S=500.2=1000N Do không ma sát nên ta thực hiện một lực kéo là 125N vậy chiều dài mpn là : 1000:125=8 (m) b) Công của lực kéo thực tế là: Atp = 150 . 8 = 1200 (J)
Hiệu suất: H = A : Atp . 100 = (1000 : 1200) .100=83,3%
a. Công: A = F.s = 50.10.2 = 1000N
Chiều dài mpn: \(l=\dfrac{A}{F}=\dfrac{1000}{125}=8m\)
b. Công toàn phần: Atp = F'.l = 25.8 = 200J
Hiệu suất mpn:
\(H=\dfrac{A_i}{A_{tp}}=\dfrac{1000}{200}.100\%=5\%\)

Chọn đáp án A
Công thức của lực ma sát trượt: F m s t = μ t N ⇀
μ t : Hệ số ma sát trượt, không có đơn vị, phụ thuộc vào vật liệu và tình trạng của các mặt tiếp xúc.
N: áp lực của vật lên bề mặt tiếp xúc.

Chọn B.
Công thức của lực ma sát trượt: Fmst = tN.
μt: Hệ số ma sát trượt, không có đơn vị, phụ thuộc vào vật liệu và tình trạng của các mặt tiếp xúc.
N: áp lực của vật lên bề mặt tiếp xúc.

Biểu thức xác định của lực ma sát trượt là: F m s t = μ t N
Đáp án: A

Chọn B.
Vật trượt lên với tốc độ không đổi bởi lực dọc theo mặt phẳng nghiêng nên theo định luật II Niu-tơn có:
F = Psin30 + Fms = mg(sin30o + cos30o )
⟹ AF = Fℓ = mg(sin30o + cos30o)ℓ = mg(sin30o + cos30o) h sin 30 0


Chọn B.
Vật trượt lên với tốc độ không đổi bởi lực F ⇀ dọc theo mặt phẳng nghiêng nên theo định luật II Niu-tơn có:
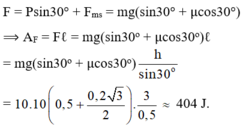

Lại một lần nữa.
Bg
Cách 1: Tự thay thế các số đo. Cạnh hình lập phương là 1 cm --> Thể tích: 1 cm3. Rồi tự tăng cạnh lên 2%,.... Đây là cách dễ nhất. Từ đó, bạn thấy thể tích của nó tăng \(\frac{51}{50}\times\frac{51}{50}\times\frac{51}{50}\)(tự tính)
Cách 2:"Phức tạp":
Gọi a là cạnh của hình lập phương (hlp) đó. (a là số tự nhiên)
=> a x a x a là thể tích của hlp
a + a x 2%
= a x 1 + a x 2%
= a x (1 + 2%)
= a x \(\frac{51}{50}\)
=> Thể tích mới của hlp: a x \(\frac{51}{50}\)x a x \(\frac{51}{50}\)x a x \(\frac{51}{50}\)= a x a x a x \(\frac{51}{50}\)x \(\frac{51}{50}\)x\(\frac{51}{50}\)
Mà a x a x a chính là thể tích ban đầu.
=> Thể tích mới sẽ gấp \(\frac{51}{50}\)x \(\frac{51}{50}\)x \(\frac{51}{50}\)
Vậy...