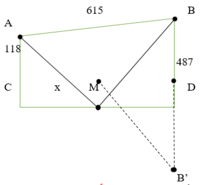
Một con kênh có 2 bờ song song. P, Q là hai điểm cố định nằm ở hai phía con kênh. Xác định cầu MN vuông góc với kênh để đoạn đường đi từ P đến N bằng đoạn đường đi từ Q đến M (N nằm ở bờ kênh phía P còn M nằm ở bờ kênh phía Q).
Giúp em với ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 10 2018
Chọn A.
Phương pháp:
Lấy A’ đối xứng với A qua bờ sông, nối A’B cắt bờ sông tại M khi đó ta có AM + MB = A’B là quãng đường ngắn nhất mà người đó đi.
Sử dụng định lý Pytago và định lý Ta-lét để tính toán.
Cách giải:
CM
15 tháng 7 2019
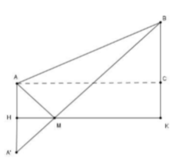
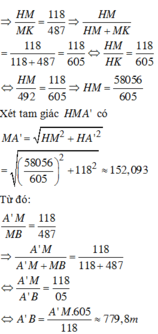
Đáp án C
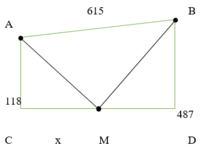
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD 
Từ đề bài ta có: f (x) = 
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) =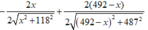 
=> f’(x) = 0
Ta có bảng biến thiên
| x |
0 |
0 |
492 |
| y’ |
|
+ 0 - |
|
| y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇔ AM + MB ngắn nhất
⇔ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng
