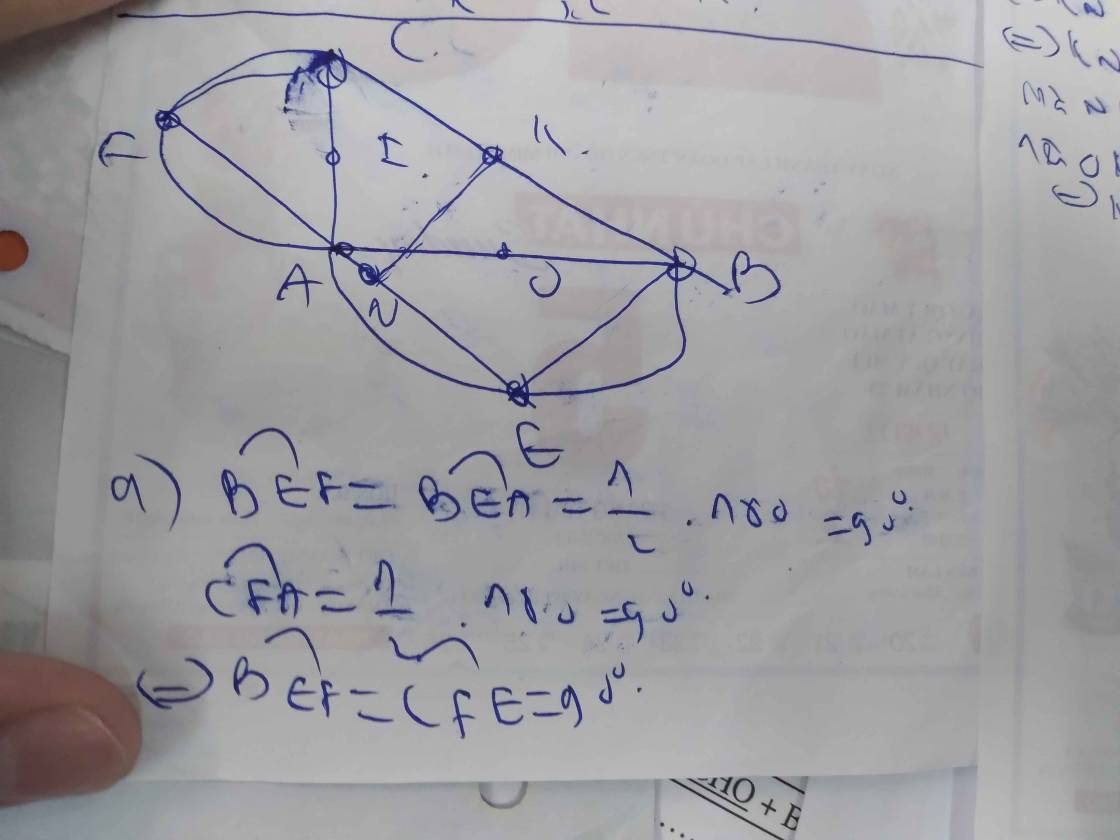
Cho tam giác ABC vuông tại A, ở bên ngoài tam giác vẽ 2 đường tròn đường kính AB, AC. Một đường thẳng d quay quanh A cắt 2 nửa đường tròn lần lượt tại M và N. Xác định M, N sao cho chu vi BCMN lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn muốn nhận giày và balo miễn phí cho năm học mới? --->Tham gia ngay Minigame NHANH NHƯ CHỚP số thứ 7 ngày 16/02/2019 tại đây: https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b Cơ hội rất hiếm! Hôm qua bạn Thiên An vừa nhận được 1 balo trị giá 350k đấy! Xem chi tiết :https://alfazi.edu.vn/question/5c6818c4641b064a18a2575b
ALFAZI THƯƠNG HIỆU HỌC TẬP SỐ 1 VN!
a) Ta thấy: Các góc ^AMB, ^ANC nội tiếp chắn nửa đường tròn => ^AMB = ^ANC = 900
=> BM và CN cùng vuông góc MN => BM // CN
Xét tứ giác BMNC: BM // CN, ^BMN = ^CNM = 900 => Tứ giác BMNC là hình thang vuông.
b) Gọi AK là trung tuyến từ đỉnh A của \(\Delta\)ABC. Dễ thấy IK là đường trung bình hình thang BMNC
=> IK // BM // CN. Mà BM,CN vuông góc MN nên IK vuông góc MN tại I => ^AIK = 900
=> I nằm trên đường tròn đường kính AK . Do AK cố định nên (AK) cố định
=> I chạy trên đường tròn (AK). Kết luận: ...

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
nên OC là phân giác của góc MOA(1) và CM=CA
Xet (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b:
Xét ΔCOD vuông tại O có OM là đường cao
nên MC*MD=OM^2
c: \(AC=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)