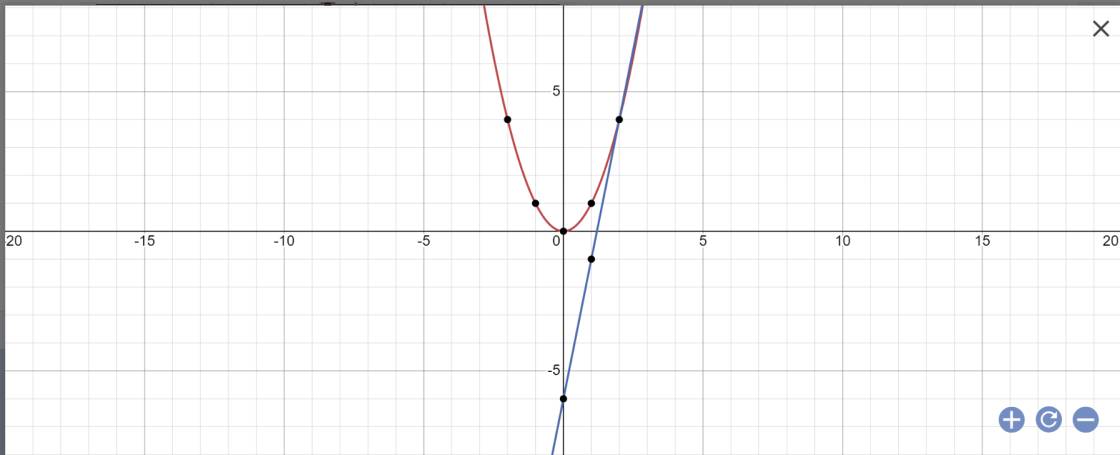
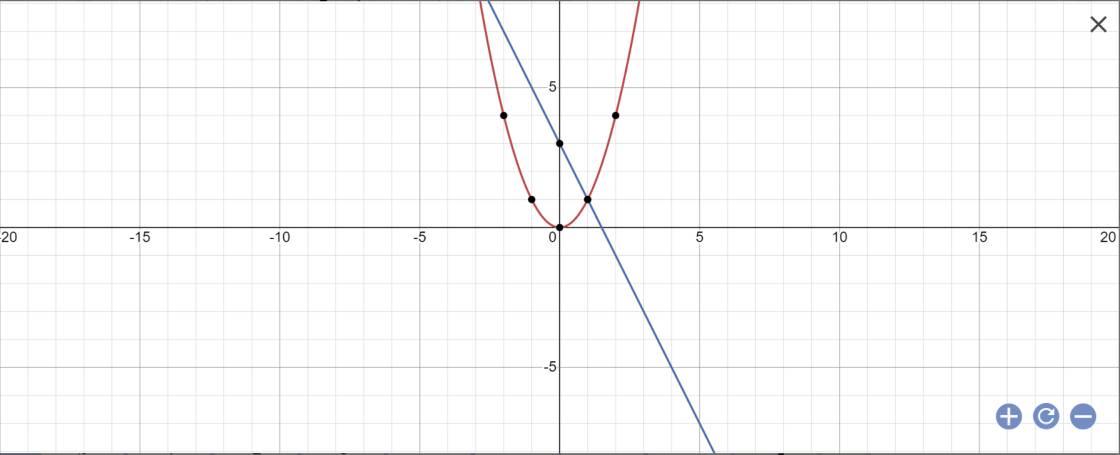
Cho hàm số y = -\(\dfrac{3}{2}\)x\(^2\) có đồ thị (P) và y = -2x + \(\dfrac{1}{2}\) có đồ thị (d)
1/ Vẽ (P) và (d) trên cùng một hệ trục tọa độ vuông góc. Xác định tọa độ các giao điểm của (P) và (d).
2/ Tìm tọa độ những điểm trên (P) thỏa tính chât tổng hoành độ và tung độ của điểm đó bằng -4.