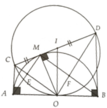
cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đtron (\(M\ne B\)
tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường trong (O) lần lượt tại C và D.
a. CMR tứ giác ACMO nội tiếp
b. CMR \(\widehat{CAM}=\widehat{ODM}\)
C. Gọi E là giao điểm của AM và BD; F là giao điểm của AC và BM. P là giao điểm của BA và DC. CM: E; F; P thẳng hàng