Question

[[柠檬]๛Čɦαŋɦ ČŠツ]

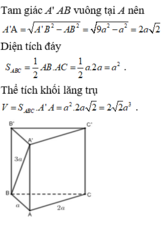
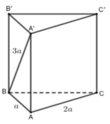
a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?

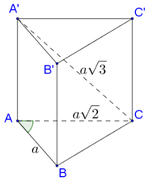
b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?

Answer 1

[Nguyễn Lê Phước Thịnh]

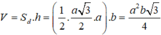
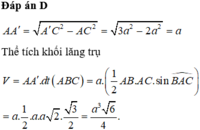
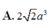
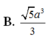
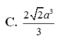
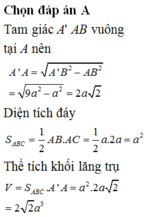
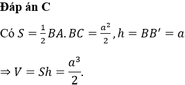
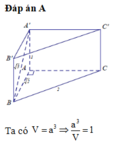
a: BB'=2a^2:a=2a

V=BB'*S ABC

=2a*1/2a^2

=a^3

Answer 2

[Minh Nguyen]

a) Với hình lăng trụ đứng ABC.ABC, diện tích tứ giác ABBA bằng 2a^2 và đáy ABC là tam giác vuông cân tại A, ABa. Thể tích khối lăng trụ ABC.ABC có thể tính bằng công thức: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Vì đáy ABC là tam giác vuông cân nên diện tích đáy là \(\frac{1}{2} \times a \times a = \frac{1}{2}a^2\). Chiều cao của lăng trụ chính là cạnh AB, vì tam giác ABa là tam giác vuông cân nên \(AB = \sqrt{2}a\). Do đó, thể tích khối lăng trụ ABC.ABC là: \(V = \frac{1}{3} \times \frac{1}{2}a^2 \times \sqrt{2}a = \frac{\sqrt{2}}{6}a^3\). b) Với hình lăng trụ đứng ABC.ABC, góc giữa (ABC) và (ABC) bằng 60°, ta cũng áp dụng công thức tính thể tích khối lăng trụ: \(V = \frac{1}{3} \times \text{Diện tích đáy} \times \text{Chiều cao}\). Diện tích đáy và chiều cao đã được tính tương tự như phần a), ta có thể tính được thể tích khối lăng trụ ABC.ABC.