Cho 8,3 (g) hỗn hợp rắn A gồm Fe và Al vào dung dịch 200 ml CuSO4 1,05M. Khi phản ứng xảy ra hoàn toàn được 15,68 (g) hỗn hợp rắn B gồm 2 kim loại và dung dịch X. Tính % khối lượng mỗi chất có trong hỗn hợp rắn A.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 11 2021
a, 2Al + 3CuSO4 → Al2(SO4)3 + 3Cu
x…………3/2.x
Fe + CuSO4 → FeSO4 + Cu
y……..y
Al phản ứng hết với CuSO4 sau đó Fe mới phản ứng với CuSO4. Vì sau phản ứng thu được rắn Y gồm 2 kim loại nên Al đã tan hết và Fe có thể đã phản ứng 1 phần hoặc chưa phản ứng. 2 kim loại trong Y là Fe và Cu.
⇒ nCu = nCuSO4 = 0,2.1 = 0,2 mol
⇒ mFe dư = mY - mCu = 15,68 - 0,2.64 = 2,88g
Đặt số mol Al ban đầu là x, số mol Fe phản ứng là y, ta có hệ phương trình:
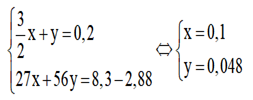
⇒ mAl = 0,1.27 = 2,7g
⇒ %mAl = 2,7/8,3.100 = 32,53%
15 tháng 7 2017
2 A l + 3 C u S O 4 → A l 2 S O 4 3 + 3 C u
x…………3/2.x
F e + C u S O 4 → F e S O 4 + C u
y……..y
Al phản ứng hết với C u S O 4 sau đó Fe mới phản ứng với C u S O 4 . Vì sau phản ứng thu được rắn Y gồm 2 kim loại nên Al đã tan hết và Fe có thể đã phản ứng 1 phần hoặc chưa phản ứng. 2 kim loại trong Y là Fe và Cu.
⇒ n C u = n C u S O 4 = 0,2.1 = 0,2 mol
⇒ m F e dư = m Y - m C u = 15,68 - 0,2.64 = 2,88g
Đặt số mol Al ban đầu là x, số mol Fe phản ứng là y, ta có hệ phương trình:
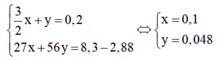
⇒ m A l = 0,1.27 = 2,7g
⇒ % m A l = 2,7/8,3.100 = 32,53%
⇒ Chọn A.
16 tháng 9 2019
Chọn B.
Sau phản ứng thu được chất rắn A gồm hai kim loại, chứng tỏ còn dư Fe và hai kim loại là: Fe và Cu.
Ta có: mkim loại = mCu + mFe = 64.0,075 + 56nFe dư = 9 gam.
⇒ nFe dư = 0,075 mol.
Dùng lượng HNO3 ít nhất để hòa tan A thì dung dịch thu được gồm (Cu2+, Fe2+).
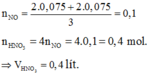
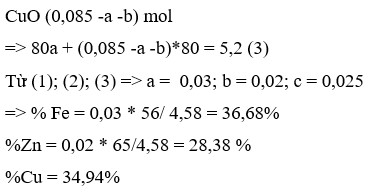
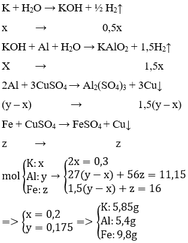
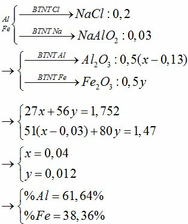
2 kim loại gồm Fe, Cu
\(n_{Al}=a;n_{Fe\left(pư\right)}=b;n_{Fe\left(dư\right)}=c\\ 27a+56\left(b+c\right)=8,3\\ n_{Cu}=0,2.1,05=0,21=1,5a+b\\ m_X=56c+64.0,21=15,68\\ a=0,1;b=0,06;c=0,04\\ \%m_{Al}=\dfrac{27a}{8,3}.100\%=32,53\%\\ \%m_{Fe}=67,47\%\)