Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2021
Do S.ABCD là chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\)
Mà \(O\in AC\Rightarrow SO\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2021
Do S.ABCD là chóp tứ giác đều \(\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\)
Mà \(AC\perp BD\) (hai đường chéo hình vuông)
\(\Rightarrow AC\perp\left(SBD\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b. Qua B kẻ đường thẳng song song AC cắt DC kéo dài tại E
\(\Rightarrow AC||\left(SBE\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SBE\right)\right)=d\left(H;\left(SBE\right)\right)\)
\(\left\{{}\begin{matrix}AC\perp\left(SBD\right)\\AC||BE\end{matrix}\right.\) \(\Rightarrow BE\perp\left(SBD\right)\)
Trong tam giác vuông SBH, từ H kẻ \(HK\perp SB\Rightarrow HK\perp\left(SBE\right)\)
\(\Rightarrow HK=d\left(H;SBE\right)\)
\(BD=a\sqrt{2}\Rightarrow BH=\dfrac{BD}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{3}}{2}\)
ÁP dụng hệ thức lượng:
\(HK.SB=SH.BH\Rightarrow HK=\dfrac{SH.BH}{SB}=\dfrac{a\sqrt{30}}{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
a.
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
Mà \(AC\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b.
\(SO\perp\left(ABCD\right)\Rightarrow OC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\)
\(tan\widehat{SCO}=\dfrac{SO}{OC}=\sqrt{3}\Rightarrow\widehat{SCO}=60^0\)
c.
Gọi E là trung điểm CD, từ O kẻ \(OF\perp SE\)
OE là đường trung bình tam giác BCD \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}BC=a\\OE||BC\Rightarrow OE\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SOE\right)\)\(\Rightarrow CD\perp OF\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Do \(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF\)
Hệ thức lượng: \(OF=\dfrac{OE.SO}{\sqrt{OE^2+SO^2}}=...\)
17 tháng 6 2023
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
CM
9 tháng 6 2019
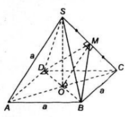
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
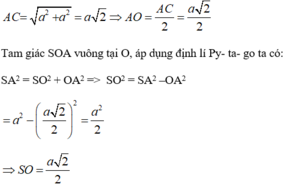
=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o
6 tháng 7 2023
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
30 tháng 4 2022
Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...
28 tháng 4 2016
1.SA \(\perp\)AB , SA\(\perp\)AD =>SAB vuông tại A, SAD vuông tại A
\(\begin{cases}AB\perp BC\left(hvABCD\right)\\SA\perp BC\left(SA\perp mpABCD\right)\end{cases}\) =>(SAB)\(\perp\)BC =>SB\(\perp\)BC =>SBC vuông tại B
\(\begin{cases}AD\perp CD\\SA\perp CD\end{cases}\) =>(SAD)\(\perp\)CD =>SD\(\perp\)CD =>SCD vuông tại D
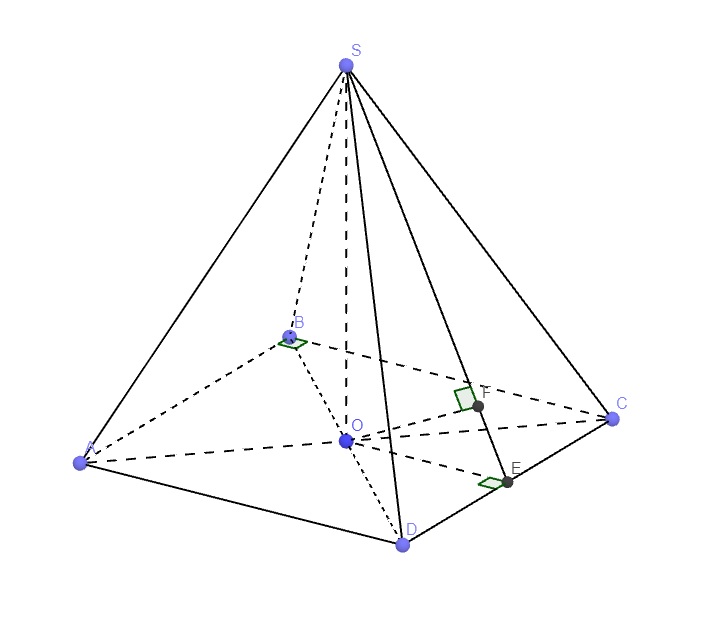
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
b: AC vuông góc BD
BD vuông góc SO
=>BD vuông góc (SAC)
=>(SBD) vuông goc (SAC)