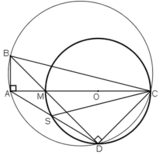
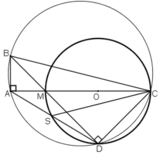
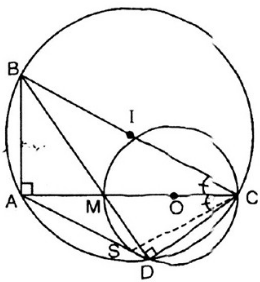
Cho tam giác ABC vuông trên AC lấy M vẽ ( O, MC/2) Kẻ BM cắt đường tròn tại D . Đường thẳng DA cắt đường tròn tại S
CMR a) ABCD nội tiếp
b) góc ACB bằng góc ACS
c) tính diện tích chu vi của đường tròn ngoại tiếp tứ giác ABCD
biết AB= 9 , AC=12

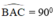 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
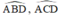 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 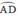
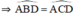
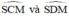 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 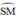
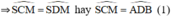
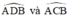 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 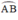
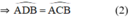

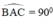 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.

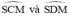 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 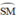
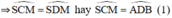
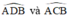 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 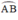
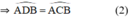

[ Tự kẻ hình ]
a, Vì góc MDC là góc nội tiếp chắn nửa đtron ( O )
=> góc MDC = 90độ
Xét tứ giác ABCD có gócMDC = góc ABC ( cùng = 90độ )
Mà 2 góc này cùng nhìn cạnh BC => Tgiac ABCD nt
b, Vì tgiac ABCD nt
=> góc ADB = góc ACB ( 2 góc cùng chắn cug AB )
Mà góc ADB = góc SCM ( 2 góc nt cùng chắn cug SM của đt ( O ) )
=> Góc ACB = góc SCM
c, xét tam giác ABC
AD định lý pytago : AB2 + AC2 = BC2
=> BC = 15 .
Chu vi của đtron ngoại tiếp : C = π.d = 3,14× 15 = 47,1
^^ Nếu đúng thì né :) đừng chép âm thầm