Trong mặt phẳng tọa độ Oxy cho đường thẳng d 4x+2y+1=0 và điểm A(1;1)
Xác định tọa độ hình chiếu vuông góc của Alên d.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)

Đáp án A
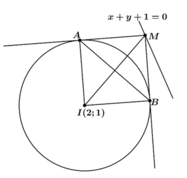
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
![]()
- Ta có :
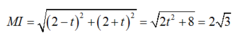
- Do đó : 2t2+ 8= 12
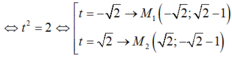

(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)

Cách 1:
Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)
Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)
\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)
\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)
\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)
Dấu "=" xảy ra khi và chỉ khi:
\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)
\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Cách 2:
Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)
Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:
\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)
Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)
\(\Rightarrow C\left(2;2\right)\)
Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)
Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)
\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD
\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Gọi \(AH\) là hình chiếu của \(A\) trên \(d\)
\(\Rightarrow AH:-2x+4y+c'=0\)
AH đi qua \(A\left(1;1\right)\Rightarrow-2.1+4.1+c'=0\)
\(\Rightarrow c'=-2\)
\(\Rightarrow\) phương trình \(AH\) là : \(-2x+4y-2=0\Rightarrow-x+2y-1=0\)
Tọa độ H là nghiệm của hệ phương trình :
\(\left\{{}\begin{matrix}-x+2y-1=0\\4x+2y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{5}\\y=\dfrac{3}{10}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\)
Gọi \(\left(d'\right)\) là đường thẳng qua A và vuông góc với (d). Do (d) có VTPT \(\overrightarrow{n_d}=\left(4;2\right)\)
\(\Rightarrow\) \(\left(d'\right)\) có VTPT \(\overrightarrow{n_{d'}}=\left(2;-4\right)\) hay \(\left(d'\right):2x-4y+m=0\) \(\left(m\inℝ\right)\)
Mà \(A\left(1;1\right)\in\left(d'\right)\) nên \(2-4+m=0\Leftrightarrow m=2\). Vậy đường thẳng qua A và vuông góc với \(d\) có pt là \(2x-4y+2=0\) hay \(x-2y+1=0\)
Do đó hình chiếu vuông góc H của A lên d chính là giao điểm của d' và d. Nếu \(H\) có tọa độ \(\left(x_H;y_H\right)\) thì \(x_H;y_H\) thỏa mãn hệ phương trình \(\left\{{}\begin{matrix}x_H-2y_H+1=0\\4x_H+2y_H+1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_H=-\dfrac{2}{5}\\y_H=\dfrac{3}{10}\end{matrix}\right.\)\(\Rightarrow H\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\).
Vậy hình chiếu của A lên d có tọa độ \(\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\)