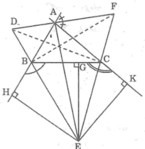
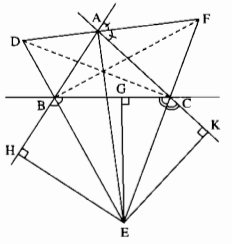
Bài 1: Cho tam giác ABC , các đường phân giác của góc ngoài tai B và C cất nhau ở E . Gọi G,H,K thứ tự là chân các đường vuông góc kẻ từ E đến các đường thẳng BC,AB,AC
a) có nhận xét gì về các độ dài EH , EG , EK
b) CM AE là phân giác của góc BAC
c) Đường phân giác của góc ngoài tại A của tam giác ABC cắt các đường thẳng BE, CEtaij D, F . CMR EA vuông góc với DF
d) Các đường AE, BF , CD là các đường gì trong tam giác ABC
e) Các đường EA , FB , DC là các đường gì trong tam giác DEF
Mình làm được câu a,b,c rồi còn 2 câu d,e nữa rất mong các bạn giải giúp mình 2 câu cuối
Bài 2 : Cho tam giác ABC vuông tại A . vé đường cao AH . trên cạnh BC lấy điểm Dsao cho BD =BA
a) CM góc BAD = góc ADB
b) CM AD là phân giác của góc HAC
c) vẽ DK vuông góc với AC (K\(\in\)AC) . CM AK =AH
d) CM AB+AC < BC + 2AH
Mình mới làm được câu a , mấy câu còn lại mong các bạn giúp mình nhé ! Bạn nào làm nhanh nhất mình sẽ tích cho bạn đó . Cảm ơn nhiều .hi hi !!