Có thể lập được bao nhiêu số tự nhiên có 3 chử số khác nhau chọn từ tập A = { 1;2;3;4;5 } sao cho mỗi số lập được luôn có mặt chữ số 3 ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)
CM
20 tháng 4 2019
Đáp án B
Phương pháp: Xét từng trường hợp a = 3; b = 3; c = 3 rồi cộng các kết quả ta được số các số cần tìm.
Cách giải: Gọi số có ba chữ số là a b c ¯ .
- TH1: a = 3.
Có 4 cách chọn b và 3 cách chọn c nên có 4.3 = 12 số.
- TH2: b = 3
Có 4 cách chọn a và 3 cách chọn c nên có 4.3 = 12 số.
- TH3: c = 3.
Có 4 cách chọn a và 3 cách chọn b nên có 4.3 = 12 số.
Vậy có tất cả 12 + 12 + 12 = 36 số.
HP
29 tháng 12 2021
Số tự nhiên có 3 chữ số có dạng \(\overline{abc}\).
TH1: \(a=3\)
Nếu \(b=4\) thì lập được 2 số tự nhiên thỏa mãn.
Nếu \(b\in\left\{1;2\right\}\), b có 2 cách chọn, c có 4 cách chọn \(\Rightarrow\) Lập được 8 số tự nhiên thỏa mãn.
TH2: \(a\in\left\{1;2\right\}\)
a có 2 cách chọn, b có 5 cách chọn, c có 4 cách chọn.
\(\Rightarrow\) Lập được \(2.5.4=40\) số tự nhiên thỏa mãn.
Vậy lập được 48 số tự nhiên thỏa mãn.
AH
Akai Haruma
Giáo viên
28 tháng 10 2021
Lời giải:
Gọi số cần tìm có dạng $\overline{abc}$. Xét các TH sau:
TH1: $c=0$
$a$ có 7 cách chọn, từ $1,2,4,5,7,8,9$
$b$ có 6 cách chọn
$\Rightarrow$ có $7.6=42$ cách chọn số
TH2: $c\neq 0$
$c$ có 3 cách chọn $(2,4,8)$
$a$ có $6$ cách chọn (bỏ số 0)
$b$ có $6$ cách chọn
$\Rightarrow$ có $3.6.6=108$ cách chọn số
Từ 2 TH trên suy ra có $108+42=150$ cách chọn số.
21 tháng 4 2023
Chia A thành 3 tập hợp:
B={1;4;7}; C={2;5;8}; D={0;3;6}
TH1: 2 số trong B, 2 số trong C
=>Có \(C^2_3\cdot C^2_3\cdot4!=216\left(cách\right)\)
TH2: 1 số trong B, 1 số trong C, số 0 và 1 số trong D
=>Có 3*3*1*2*3*3*2*1=324 cách
TH3: 1 số trong B, 1 số trong C, 2 số khác 0 trong D
=>Có 3*3*1*4!=216 cách
TH4: 3 số trong B, số 0
=>Có 3*3*2*1=18 cách
TH5: 3 số trong B, 1 số khác 0 trong D
=>Có 2*4!=24*2=48 cách
TH6: 3 số trong C, số 0
=>Có 3*3*2*1=18 cách
TH7: 3 số trong C, 1 số khác 0 trong D
=>Có 2*4!=48 cách
=>Có 216+324+216+18+48+18+48=888 cách
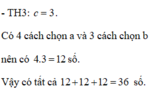
Số cách chọn là 4*3=12(cách)
Chọn 2 chữ số còn lại từ {1;2;4;5} có: \(C_4^2=6\) cách
Hoán vị 3 chữ số: \(3!=6\) cách
Tổng cộng có: \(6.6=36\) số