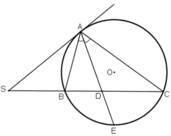
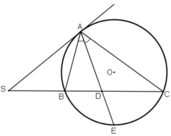
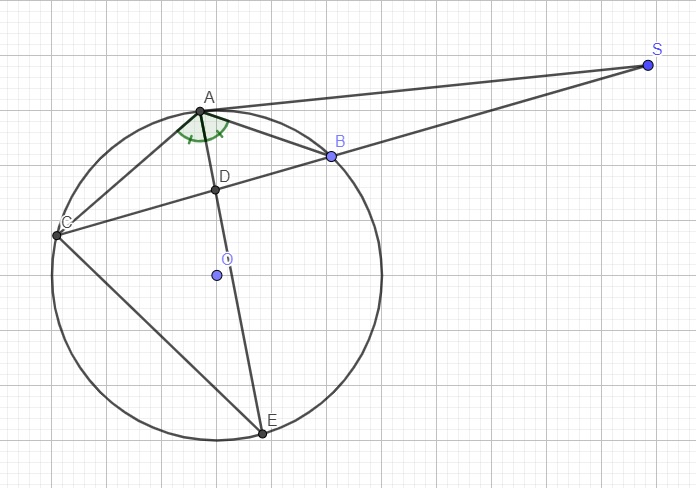
Cho đường tròn tâm O và điểm S ở ngoài đường tròn . Từ S kẻ hai tiếp tuyến SA và SD và cát tuyến SBC tới đường tròn ( B ở giữa S và C ).a) Phân giác của góc BAC cắt dây cung BC ở M . Chứng minh SA = SM .b) AM cắt đường tròn ở E. Gọi G là giao điểm của OE và BS; F là giao điểm của AD với BC . Chứng minh SA^2 = SG . SF .c) Biết SB = a ; Tính SF khi BC...
Đọc tiếp
Cho đường tròn tâm O và điểm S ở ngoài đường tròn . Từ S kẻ hai tiếp tuyến SA và SD và cát tuyến SBC tới đường tròn ( B ở giữa S và C ).
a) Phân giác của góc BAC cắt dây cung BC ở M . Chứng minh SA = SM .
b) AM cắt đường tròn ở E. Gọi G là giao điểm của OE và BS; F là giao điểm của AD với BC . Chứng minh SA^2 = SG . SF .
c) Biết SB = a ; Tính SF khi BC = \(\dfrac{2a}{3}\)
là góc có đỉnh nằm bên trong đường tròn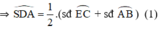
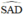là góc tạo bởi tiếp tuyến AS và dây AE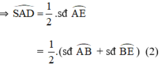
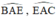lần lượt là các góc nội tiếp chắn các cung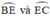 
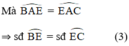
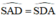
là góc có đỉnh nằm bên trong đường tròn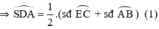
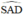là góc tạo bởi tiếp tuyến AS và dây AE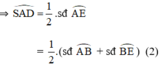
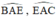lần lượt là các góc nội tiếp chắn các cung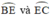 
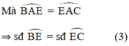
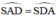
a: góc SAM=góc SAB+góc BAM
góc SMA=góc SCA+góc MAC
mà góc SAB=góc SCA và góc BAM=góc CAM
nên góc SAM=góc SMA
=>SM=SA
b: góc SGO=90 độ
Vì góc SAO=góc SGO
=>SAGO nọpi tiếp
=>góc SGA=góc SOA=1/2*góc DOA=1/2*sđ cung AD
=>góc SAD=góc SGA
=>ΔSAF đồng djng với ΔSGA
=>SA/SG=SF/SA
=>SA^2=SG*SF