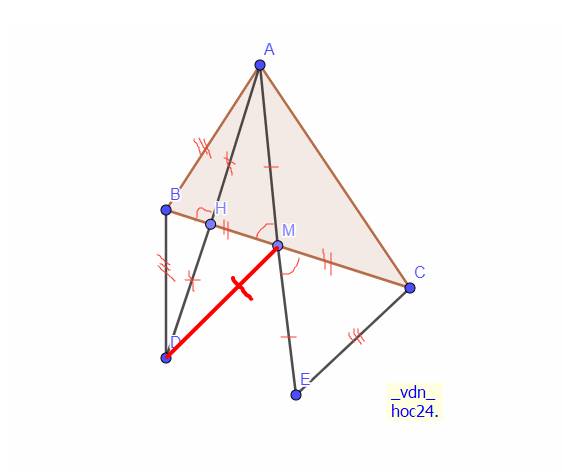
Câu 22. Cho tam giác ![]() nhọn, có AB = AC. Kẻ tia phân giác của góc BAC cắt BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Vẽ M là trung điểm của AC. Trên tia đối của tia MB lấy điểm E sao cho MB = ME.
nhọn, có AB = AC. Kẻ tia phân giác của góc BAC cắt BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Vẽ M là trung điểm của AC. Trên tia đối của tia MB lấy điểm E sao cho MB = ME.
a) Chứng minh tam giác AHB = tam giác AHC. Suy ra HB = HC
b) Chứng minh tam giác AHB = tam giác DHCSuy ra AB // CD
c) Chứng minh 3 điểm D, C, E thẳng hàng.

a: Xet ΔAHB và ΔAHC có
AB=AC
góc BAH=góc CAH
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: Xét ΔAHB vuông tại H và ΔDHC vuông tại H có
HA=HD
HB=HC
=>ΔAHB=ΔDHC
=>góc HAB=góc HDC
=>AB//CD
c: Xét tứ giác ABCE có
M là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//CE
mà CD//AB
nên C,E,D thẳng hàng