Question

[trương thị hương giang]

cho tam giác abc cân tại a . lấy điểm d thuộc cạnh ac và điểm E thuộc cạnh ab sao cho AD=AE       a)  chứng minh tam giác adb = tam giác aec                                                                                b) gọi I là giao điểm của BD và CE  . tam giác ICB là tam giác gì ? vì sao ?                                    c) chứng minh ED// BC

Answer 1

[Thuỳ Linh Nguyễn]

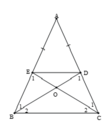
`a)` 

Có `Delta ABC ` cân tại `A(GT)=>AB=AC`

Xét `Delta ADB` và `Delta AEC` có:

`{:(AB=AC(cmt)),(hat(A)-chung),(AD=AE(GT)):}}`

`=>Delta ADB=Delta AEC(c.g.c)(đpcm)`

`b)`

Có `Delta ABC` cân tại `A=>hat(ABC)=hat(ACB)`

`=>hat(EBC)=hat(DCB)`

mà `hat(B_1)=hat(C_1)(Delta ADB=Delta AEC)`

`hat(B_1)+hat(B_2)=hat(EBC)`

`hat(C_1)+hat(C_2)=hat(DCB)`

nên `hat(B_2)=hat(C_2)`

`=>Delta IBC` cân tại `I` 

`c)`

Có `AE=AD(GT)=>Delta AED` cân tại `A`

`=>hat(E_1)=(180^0-hat(A))/2(1)`

`Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2(2)`

Từ `(1)` và `(2)=>hat(E_1)=hat(ABC)`

mà `2` góc này ở vị trí đ/vị 

nên `ED////BC(đpcm)`

Answer 2

[trương thị hương giang]

c.ơn nha